Г л а в а II

ПРОСТЕЙШИЕ СЛУЧАИ ДВИЖЕНИЯ

ТВЕРДОГО ТЕЛА

 

§ 9. Поступательное движение твердого тела

 

Поступательным движением твердого тела называется такое его движение, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению во все время движения.

Теорема. При поступательном движении твердого тела все его точки дви­жутся по одинаковым и параллельным траекториям и имеют в каждый данный момент времени равные по модулю и направлению скорости и ускорения.

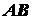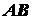Доказательство. Для доказательства теоремы рассмотрим движение отрезка прямой , проведенного в теле, совершающем поступательное движение (рис. 2.10). Из определения поступа­тельного движения следует, что в каждый данный момент времени отрезок , занимающий последовательно положения 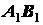, , 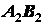  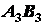и т.д., остается параллельным своему первоначальному положению. Учиты­вая это и то что 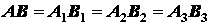, делаем вывод, что ломаные лини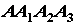и   и 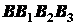  параллельны и при на­ложении совпадут всеми своими точками. При бесконечном уменьшении про­межутков времени между рассматриваемыми по­ложениями отрезка мы видим, что точка 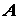  и точка  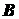 описывают одинаковые кривые, т. е. кривые, совпадаю­щие при наложении.

Для доказательства второй части теоремы заметим, что

 

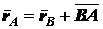.  (2.27)

 

Возьмем производные по времени от левой и правой частей

 

.

 

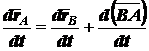Так как 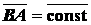, то .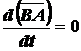

Тогда

 

;

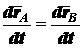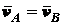;  (2.28)

;

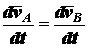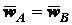. (2.29)

 

Разобранная теорема позволяет сделать вывод, что поступательное движение твердого тела вполне определяется движением какой-либо одной его точки.

 

§ 10. Понятие о вращении твердого тела вокруг неподвижной оси

 

Вращением твер­дого тела вокруг неподвижной оси называется такое движение, при котором все его точки, лежащие на некоторой прямой, называемой осью вращения, все время остаются неподвижными.

Рассмотрим вращение твердого тела (рис. 2.11) вокруг оси, проходящей через две неподвижные точк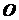и   и 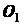. Проведем через ось 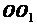  неподвижную полуплоскость  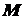 и движущуюся вместе с телом полуплоскость 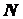. Вращение тела будет определяться величиной дву­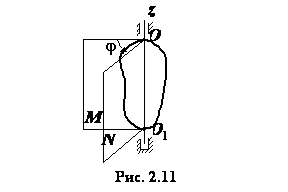гранного угла  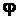 между по-луплоскостям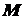и   и 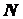. Угол  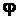 называется углом поворота. Условимся считать за положительное направление вращения тот случай, когда, смотря с заданного направления оси вращения, увеличение угла поворота наблюдается в сторону, противоположную движению часовой стрелки.

При вращении угол поворота 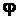  изменяется в зависимости от времени. Равенство:

 

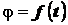 (2.30)

 

является уравнением вращения тела вокруг неподвижной оси. Оно позволяет определить положение тела в любой момент времени. Угол 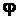  в равенстве (2.30) выражается в радианах.

 

§ 11. Угловая скорость и угловое ускорение тела

 

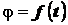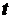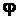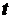 Предположим, что вращение тела вокруг неподвижной оси задано уравнением , из которого можно в момент времени   найти . Пусть через промежуток времени   после момента времени   ­угол 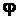  изменится на .

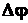Отношение приращения угла поворота 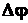  к промежутку времени , за

который произошло это приращение, называется средней угловой скоростью

 

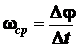. (2.31)

 

Переходя к пределу при 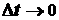, можем записать

 

;

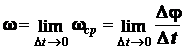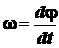. (2.32)

 

Таким образом, угловая скорость тела в данный момент времени равна первой производной от угла поворота по времени. Угловая скорость измеряется в 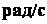  и может быть как положительной, так и отрицательной. Угловая скорость 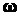  по­ложительна, если в данный момент вращение происходит против движения ча­совой стрелки, и отрицательна - в противоположном случае.

Зная зависи­мость угловой скорости 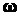  от времени 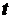, можно определить ее среднее прира­щение за единицу времени

 

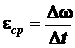.   (2.33)

 

Отношение приращения угловой скорости к приращению времени называется средним угловым ускорением.

Переходя к пределу при 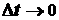, записываем

 

;

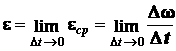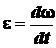.   (2.34)

 

Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое

ускорение измеряется в .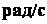

 

§ 12. Угловая скорость и угловое ускорение как векторы

 

Угловую скорость и угловое ускорение твердого тела, вращающегося вокруг неподвижной оси, можно представить в виде векторов. Вектор угловой скорости 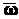  направлен по оси вращения тела в ту сторону, откуда вращение тела в дан­ный момент времени видно против хода часовой стрелки. По модулю этот вектор равен абсолютному значению 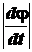. В качестве точки приложения вектора угловой скорости 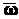  может быть принята любая точка (вектор  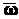 есть вектор скользящий).

Вектор углового ус­корения 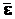  также лежит на оси вращения, совпадает по направлению с вектором угловой скорости 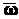  в случае ускоренного вращения (рис. 2.12, а) и направлен в противоположную сторону при замедленном вращении.

 

 

 

 

 

 

 

 

 

 

 

 

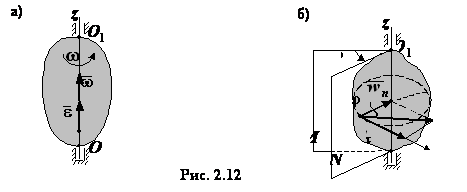
§ 13. Скорость и ускорение точки вращаю­щегося тела

 

 Возьмем в теле, вращающемся вокруг неподвижной оси, некото­рую точку 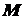, находящуюся на расстоянии 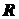  от оси вращения. При вращении тела точка  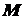 движется по окружности радиуса  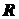 (рис. 2.12, б). Поэтому при пово­роте тела на угол  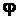 точка 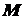  окажется на расстоянии  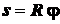 от своего на­чального положения. Дифференцируя это равенство по времени, получим

 

.

 

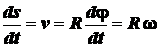Таким образом,

 

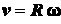, (2.35)

 

т. е. скорость любой точки вращающегося тела равна произведению расстояния от точки до оси вращения на угловую скорость. Так как скорость 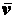  направлена по касательной к окружности, по которой движется точка 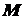, а касательная к окружности перпендикулярна к радиусу, проведенному в точку касания, то вектор 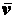  скорости любой точки вращающегося тела направлен перпендикулярно к плоскости, проходящей через точку 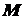  и ось вращения. Ускорение точки  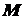 складывается из касательной и нормальной составляющих. Касательная составляющая ускорения направлена по одной прямой со скоростью и в ту же сторону, что и скорость, если движение уско­ренное, и в противоположную сторону, если движение замедленное. По фор­мулам (2.21), (2.34) и (2.35)

 

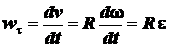. (2.36)

 

Нормальная составляющая ускорения направлена от точки 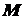  к оси вращения. Так как радиус кривизны в данном случае равен радиусу окружности, которую описывает точка, то по формулам (2.22) и (2.25)

 

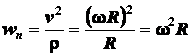. (2.37)

 

Касательное и нормальное ускорения точки вращающегося тела называются иначе вращательным 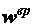  и центростремительным  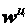 ускорениями.

 Модуль полного ускорения на основании формулы (2.23) будет равен:

 

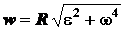. (2.38)

 

Угол 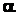, который вектор полного ускорения 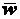  образует с радиусом ,

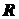определяется равенством:

 

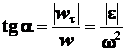. (2.39)

 

 

 

 

 

§ 14. Векторные выражения скорости и ускорения точки

вращающегося тела

 

Проведем из произвольной точки 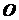  на оси вращения радиус-вектор  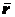 в рас­сматриваемую точку  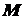 тела (рис. 2.13). Тогда

 

,

 

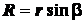поэтому

 

,

 

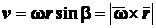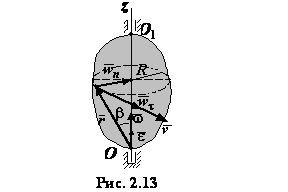где символом  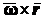 обозначено векторное произведение вектора угловой скорости  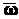 и радиуса-вектора 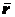. Вектор  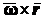 перпендикулярен к плоскости, проходящей через точку  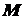 и ось вращения, и направлен в сторону вращения тела. Поэтому он совпадает с вектором скорости 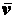  как по величине, так и по направлению. Таким образом,

 

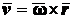.   (2.40)

 

А так как

 

,

 

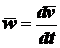то

 

 

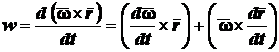
или

 

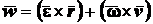. (2.41)

 

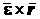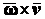Легко показать, что вектор   направлен по касательной к траектории точки в одну сторону со скоростью, если вращение ускоренное, и в противополож­ную сторону, если оно замедленное, а век­тор   направлен по радиусу к оси вра­щения. Поэтому первый из них есть вектор вращательного, а второй - центростреми­тельного ускорения точки:

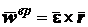; (2.42)

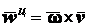. (2.43)

 

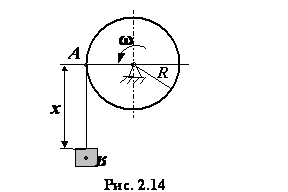
Задача 2.6. Вал радиуса 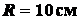  приводится во вращение гирей, привешен­ной к нему на нити. Движение гири выражается уравнением 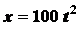, где 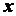  - расстояние гири от места схода нити с поверхности вала, выраженное в сантиметрах, 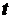  - время в секундах. Опреде­лить угловую скорость  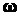 и угловое ускоре­ние  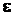 вала, а также полное ускорение вала в момент времени  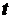 (рис. 2.14).

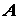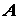Решение. Рассмотрим движение точки схода нити с поверхности вала , которая принадлежит одновременно и нити и гири. Скорость точки , принадлежащей нити, равна скорости движения гири:

 

.

 

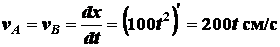Скорость точки 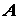  , принадлежащей валу, равна

 

.

 

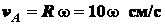Следовательно,

 

.

 

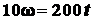Получили

 

.

 

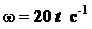Находим угловое ускорение вала

 

.

 

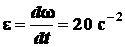Тогда полное ускорение

 

.
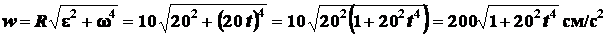