Г л а в а IV

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

 

§ 20. Относительное, переносное и абсолютное

движение точки

 

Сложным движением точки называется такое ее движение, при кото­ром она движется относительно системы отсчета, перемещающейся по отношению к некоторой другой системе отсчета, принятой за непод­вижную. Например, можно считать, что пассажир, идущий по вагону движущегося поезда, со­вершает сложное движение по отношению к полотну дороги, состоящее из движения пассажира по отношению к вагону (подвижная система отсчета) и дви­жения пассажира вместе с вагоном по отношению к полотну дороги (неподвижная система отсчета).

Движение точки по отношению к подвижной системе ко­ординат называется относительным движением точки. Скорость и ускорение этого движения называют относитель­ной скоростью и относительным ускорением и обозначают   и .

Движение точки, обусловленное движением подвижной системы координат, называется переносным движением точки.

Переносной скоростью и переносным ускорением точки на­зывают скорость и ускорение той, жестко связанной с под­вижной системой коор­динат точки, с которой совпадает в дан­ный момент времени движущаяся точка, и обозначают   и .

Движение точки по отношению к неподвижной системе координат называ­ется абсолютнымили сложным. Скорость и ускорение точки в этом движении называют абсолютной скоростью и абсолютным ускорением и обозначают   и .

В приведенном выше примере движение пассажира относительно вагона будет относительным, а скорость – относительной скоростью пассажира; движение вагона по отношению к полотну дороги будет для пассажира переносным движением, а скорость вагона, в котором находится пассажир, будет в этот момент его переносной скоростью; наконец, движение пассажира по отношению к полотну будет его абсолютным движением, а скорость – абсолютной скоростью.

 

§ 21. Определение скорости точки при сложном

движении

 

Пусть имеется неподвижная система отсчета   по отношению к кото­рой движется подвижная система отсчета . Относительно подвижной системы координат движет­ся точка   (рис. 2.26). Уравнение движения точки , находящейся в сложном движении, можно задать векторным способом

 

,   (2.67) 

 

где   - радиус-вектор точки , определяющий ее положение относительно 

 не­подвижной системы отсчета ;

 -  радиус-вектор, определяющий положение начала отсчета подвижной

 системы координат ;

 -  радиус-вектор рассматриваемой точки , определяющий ее 

 положение относительно подвижной системы координат.

Пусть   координаты точки   в подвижных осях. Тогда

,   (2.68) 

 

где 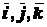  - единичные векторы, направленные вдоль под­вижных осей . Подставляя (2.68) в равенство (2.67), полу­чим:

 

.     (2.69)

 

При относительном движении координаты   изменя­ются с течением времени. Чтобы найти скорость относитель­ного движения, нужно продиффе­ренцировать радиус-вектор   по времени, учитывая его изменение только за счет относи­тельного движе­ния, то есть только за счет изменения коор­динат , а подвижную систему координат предполагать при этом неподвижной, то есть вектора 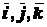  считать не зависящими от времени. Дифференцируя равенство (2.68) по времени с учетом сде­ланных оговорок, получим относитель­ную скорость:

 

 ,    (2.70)

 

где точки над величинами означают производные от этих ве­личин по времени:

 

,  ,  .

 

Если относительного движения нет, то точка   будет двигаться вместе с подвижной системой - координат и ско­рость точки будет равна переносной скорости. Таким обра­зом, выражение для переносной скорости можно полу­чить, если продифференцировать по времени радиус-вектор , считая   не за­висящими от времени:

.   (2.71)

 

Выражение для абсолютной скорости найдем, дифферен­цируя по времени , учитывая, что от времени зависят относительные координаты   и орты 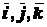  подвижной системы координат:

 

.  (2.72)

 

В соответствии с формулами (2.70), (2.71) первая скобка в (2.72) есть переносная ско­рость точки, а вторая - относитель­ная. Итак,

 

.   (2.73)

 

Равенство (2.73) выражает теорему о сложении скоростей: абсолютная скорость точки равна геометрической сумме переносной и относительной скоро­стей.

Задача 2.9. Поезд движется по прямолинейному горизонтальному пути с постоянной скоростью . Пассажир видит из окна вагона траектории капель дождя наклоненными к вертикали под углом . Определить абсолютную скорость падения дождевых капель отвесно падающего дождя, пренебрегая трением капель о стекло.

Решение. Капли дождя имеют абсолютную скорость

 

,

где   - относительная скорость капли при ее движении по стеклу вагона;

 - переносная скорость капли, равная скорости движения поезда.

Получившийся параллелограмм скоростей (рис. 2.27) диагональ делит на два равных треугольника. Рассмотрев любой из этих треугольников, находим

 

.

 

Переводим полученную скорость падения капель в :

 

.

 

§ 22. Определение ускорения точки при сложном

движении

 

Выражение для относительного ускорения точки можно получить, диффе­ренцируя относительную скорость (2.70), учи­тывая ее изменение только за счет относительного движения, то есть за счет изменения относительных координат точки , , . Вектора же 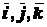  следует считать постоянными, так как движение не­движной системы координат не учитывается при определении относительной скорости и относительного ускорения точки. Итак, имеем

 

 ,   (2.74)

 

Переносное ускорение получим, дифференцируя по време­ни равенство (2.71), считая, что точка покоится по отношению к подвижной системе координат, т. е. что относительные координаты точки , ,   не зависят от времени.

 

.  (2.75)

 

Абсолютное ускорение получим, дифференцируя выраже­ние для абсолютной скорости (2.72), учитывая, что с течени­ем времени изменяются как относительные координаты , ,   точки, так и орты 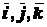  подвижной системы координат

 

 

.  (2.76)

 

Видно, что первая скобка в (2.76) есть переносное ускорение, третья - относи­тельное ускорение. Вторая скобка есть до­полнительное или кориолисово ускорение:

 

.   (2.77)

 

Итак, равенство (2.76) можно записать в виде

 

.   (2.78)

 

Эта формула и выражает теорему Кориолиса: в случае непоступательного переносного движения абсолютное ускорение точки равно векторной сумме

переносного, от­носительного и поворот­ного ускорений.

Преобразуем формулу (2.77) для ускорения Кориолиса. Для производных единичных векторов подвижной системы координат имеют место следующие формулы Пуассона:

 

;  ;  .  (2.79)

 

Здесь   - вектор мгновенной угловой скорости подвижной системы коорди­нат. Знаком   обозначено векторное произ­ведение векторов.

Подставляя формулы (2.79) в (2.77), получим:

 

. 

 

Выражение в скобках есть не что иное, как относитель­ная скорость (см. (2.70)). Окончательно получим:

 

.   (2.80)

 

Итак, ускорение Кориолиса равно удвоенному векторно­му произведению мгновенной угловой скорости подвижной системы координат на вектор отно­сительной скорости.

По общему правилу определения направления, векторного произведения имеем: ускорение Кориолиса направлено пер­пендикулярно плоскости, прохо­дящей через вектора   и  в ту сторону, откуда поворот вектора   к вектору   на меньший угол виден против хода часовой стрелки (рис. 2.28).

Из формулы (2.80) вытекает также, что величина ускоре­ния Кориолиса

 

.    (2.81)

 

Отсюда следует, что ускорение Кориолиса равно нулю в трех случаях:

1) если , т. е. в случае поступательного переносного движения или в моменты обращения в нуль угловой скорости непоступательного перенос­ного движения;

2) если , т.е. в случае относительного покоя точки или в моменты об­раще­ний в нуль относительной скорости точки;

3) если , т. е. в случае, когда вектор относительной скорости то­чки параллелен вектору угловой скорости переносного движения , как, напри­мер, при движении точки вдоль образующей цилиндра, вращающе­гося вокруг своей оси.

Задача 2.10. По железнодорожному пути, проложенному по параллели северной ши­роты, движется тепловоз со скоростью   с запада на восток. Найти корио­лисово ускорение   тепловоза.

Решение. Пренебрегая размерами тепло­воза, будем рассматривать его как некоторую точку (точка   на рис. 2.29).  Точка совершает сложное движение. За переносное движение примем враща­тельное движение точки   вместе с Землей, а за относительное движение – движение этой точки по отношению к Земле с постоянной скоростью .

Величина ускоре­ния Кориолиса согласно (2.81) равна

 

,

где   - угловая скорость вращения Земли.

 Найдем угловую скорость вращения Земли. За сутки Земля делает один оборот. Угол, соответствующий одному обороту, равен   и число секунд в сутках равно , отсюда

 

.

 

Положение и направление вектора ускорения Кориолиса определяем по об­щему правилу определения направления векторного произведения. Вектор ускорения Кориолиса   находится на прямой , так как он должен быть перпендикулярен векторам   и ,  и направлен в сторону противополож­ную направлению векторов   и .

Следовательно,

 

.

 

Задача 2.11. Точка   движется со скоростью   по окружности обода диска диаметра . Диск вращается в про­тивоположном направлении, имея в данный момент угловую скорость   и угловое ускорение   (рис. 2.30). Определить абсо­лютное ускорение точки.

Решение. Точка   совершает сложное движение. За переносное движение примем движение точки   вместе с диском, а за относительное движение – движение этой точки по отношению к диску с постоянной скоростью . Абсолютное ускорение точки   определяется по формуле (2.78)

 

.

 

Так как переносное движение точки   является вращательным, то

 

.

 

Траекторией переносного движения является окружность обода, поэтому переносное вращательное ускорение точки   направлено по касательной к этой окружности, а его модуль

 

.

 

Переносное центростремительное ускорение точки   направлено по ра­диусу к центру окружности, а его модуль

 

.

 

Траекторией относительного движения точки также является окруж­ность обода. Так как относительное движение точки   - движение равномер­ное (без ускорения) по условию, то относительное касательное ускорение равно нулю:

 

.

 

Относительное нормальное ускорение точки   направлено по радиусу к центру кривизны траектории относительного движения, а его модуль

 

.

 

Величина ускоре­ния Кориолиса согласно (2.81) равна

 

.

 

Положение и направление вектора ускорения Кориолиса определяем по об­щему правилу определения направления векторного произведения. Вектор ускорения Кориолиса   находится на прямой , так как он должен быть перпендикулярен векторам   и ,  и направлен в сторону противополож­ную направлению векторов   и .

 Проектируя все составляющие абсолютного ускорения   на оси   и , направленные по касательной к окружности и радиусу , получаем

 

;

.

 

Зная проекции абсолютного ускорения, по формуле

 

 

находим величину ускорения   в данной задаче

 

.

 

Определим направление вектора абсолютного ускорения :

 

,

 

и, следовательно,

 

 ,

 

т.е. абсолютное ускорение направлено под углом   к радиусу окружности.