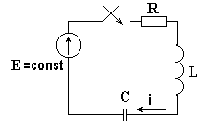
При последовательном соединении
сопротивления R, катушки индуктивности L и конденсатора С образуется
электрический R-L-C контур (рис. 8.9).
Дифференциальное уравнение для тока в контуре
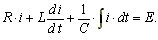 .
.
После дифференцирования
по t и деления на L получим
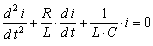 . (8.4)
. (8.4)
 Решение уравнения (8.4) равно сумме принужденной и свободной
составляющих
Решение уравнения (8.4) равно сумме принужденной и свободной
составляющих
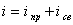 .
.
В нашем случае принужденная составляющая переходного
тока равна нулю, так как в схеме имеется емкость, являющаяся разрывом
цепи для постоянного тока.
Рис. 8.9
Свободная составляющая является
общим решением уравнения
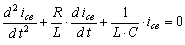 . (8.5)
. (8.5)
Пусть
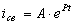 ,
, 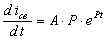 ,
,
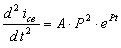 .
.
После подстановки этих выражений
в уравнение (8.5) получим характеристическое уравнение
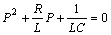 .
.
Характеристическое уравнение
имеет два корня
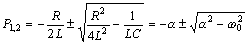 ,
,
где 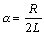 - коэффициент затухания;
- коэффициент затухания;
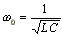 - угловая резонансная частота контура без потерь.
- угловая резонансная частота контура без потерь.
Получим
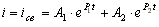 .
.
Вид корней зависит от отношения
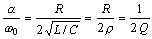 ,
,
где 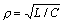 - характеристическое или волновое сопротивление контура;
- характеристическое или волновое сопротивление контура;
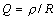 - добротность контура.
- добротность контура.
Колебательный режим
Наиболее важен часто встречающийся
случай, когда корни P1,2 - комплексные сопряженные с отрицательной
вещественной частью, свободная составляющая имеет вид затухающих колебаний.
В этом случае
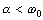 ,
,
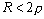 ,
, 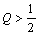 ,
,
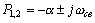 ,
,
где 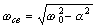 -
угловая частота собственных колебаний в контуре;
-
угловая частота собственных колебаний в контуре;
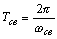 - период собственных колебаний.
- период собственных колебаний.
Ток в цепи
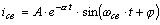 , (8.6)
, (8.6)
где А и φ - постоянные
интегрирования.
До коммутации ток в индуктивности
равен нулю, сразу после коммутации остается равным нулю
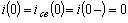 .
.
Чтобы определить две постоянные
интегрирования, необходимо иметь два начальных условия и составить два
уравнения. Напряжение на индуктивности
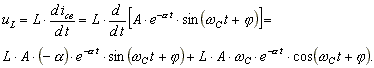 . (8.7)
. (8.7)
где 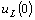 - напряжение на индуктивности в момент коммутации, является зависимым
начальным условием. Составим уравнение по второму закону Кирхгофа для
момента коммутации, чтобы определить зависимое начальное условие
- напряжение на индуктивности в момент коммутации, является зависимым
начальным условием. Составим уравнение по второму закону Кирхгофа для
момента коммутации, чтобы определить зависимое начальное условие 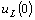 .
.
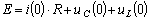 .
.
До коммутации конденсатор
был не заряжен, поэтому
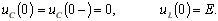 .
.
Подставляя в (8.6) и (8.7) t =
0 и используя независимое и зависимое начальные условия, получим систему
уравнений
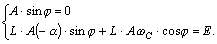 (8.8)
(8.8)
Решив систему (8.8), определим
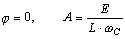
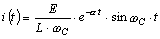 .
.
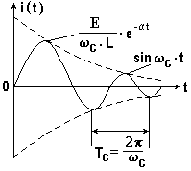 На рис. 8.10 приведена кривая изменения тока в контуре
при подключении к нему источника постоянной ЭДС. Из рисунка видно, что
колебания в контуре затухают по показательному закону из-за потерь электрической
энергии в сопротивлении R. Затухание происходит тем медленнее, чем меньше
коэффициент затухания α .
На рис. 8.10 приведена кривая изменения тока в контуре
при подключении к нему источника постоянной ЭДС. Из рисунка видно, что
колебания в контуре затухают по показательному закону из-за потерь электрической
энергии в сопротивлении R. Затухание происходит тем медленнее, чем меньше
коэффициент затухания α .
Рис. 8.10
Постоянная времени переходного
процесса 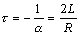 .
.
При малом коэффициенте затухания
величина ωС незначительно отличается от резонансной
частоты ω0.
Относительное затухание колебаний характеризуется
декрементом затухания, представляющим отношение мгновенных значений
тока через один период.
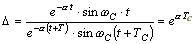 .
.
Натуральный логарифм этого
оператора носит название логарифмического декремента затухания
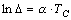 .
.
Для контура с небольшим
затуханием, когда 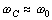
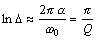
Апериодический режим в R-L-C контуре
наблюдается при большом затухании, когда 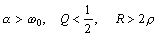 .
В этом случае корни P1,2 вещественные, отрицательные, различные.
.
В этом случае корни P1,2 вещественные, отрицательные, различные.
Свободный ток определяется
по формуле
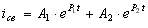 . (8.9)
. (8.9)
Напряжение на индуктивности
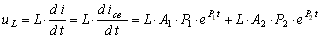 . (8.10)
. (8.10)
Подставив в уравнение (8.9) и (8.10)
t = 0 и используя независимое и зависимое условия, получим систему уравнений
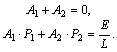
Решив эту систему, определим
постоянные интегрирования
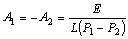 .
.
Выражение для тока в контуре
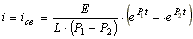
состоит из положительной, медленно затухающей экспоненты
с коэффициентом затухания P1 и отрицательной, быстро затухающей
экспоненты P2 (рис. 8.11).
 Ток получается неколебательным, он не принимает отрицательных
значений, то есть не меняет своего направления.
Ток получается неколебательным, он не принимает отрицательных
значений, то есть не меняет своего направления.
На границе между колебательным и апериодическим
режимом при
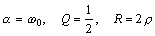
наблюдается предельный случай апериодического процесса.
Рис. 8.11