Г л а в а
I
ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ
§ 1. Абсолютно твердое тело. Сила. Система сил
Абсолютно твердым телом называется материальное тело, в котором расстояния между
точками остаются неизменными независимо от действующих сил. Несмотря на такую
абстракцию, методами статики твердого тела могут быть решены задачи о равновесии
реальных деформируемых тел.
 Сила - количественная мера механического взаимодействия материальных
тел, характеризующаяся величиной, направлением и точкой приложения. Сила является
векторной величиной. Прямая, по которой направлен вектор
силы
Сила - количественная мера механического взаимодействия материальных
тел, характеризующаяся величиной, направлением и точкой приложения. Сила является
векторной величиной. Прямая, по которой направлен вектор
силы 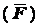 ,
называется линией действия силы (рис. 1.1).
,
называется линией действия силы (рис. 1.1).
Совокупность сил, приложенных к одному или нескольким твердым телам,
называется системой сил. Системы сил, оказывающие на твердое тело одинаковые
действия, называются эквивалентными системами. Если существует одна сила,
эквивалентная некоторой системе, то она называется равнодействующей этой
системы.
Твердое тело, которое может занимать в пространстве любое произвольное
положение, называется свободным. Если же свобода перемещения тела в пространстве
ограничена другими телами, то данное тело называется несвободным, а ограничивающие
его тела - связями. Силы, с которыми связи действуют на данное тело, называются
реакциями связей. Например, опоры моста, на которые опирается пролетное
строение, являются
для последнего
связями, а силы, с которыми они действуют на пролетное строение – реакциями этих
опор. Силы, не являющиеся реакциями связей, называются задаваемыми, или активными.
Система сил называется уравновешенной, если ее приложение к
покоящемуся свободному твердому телу не нарушает его состояния покоя.
Силы, приложенные к телу во всех точках части поверхности или во всех
точках объема тела, называются распределенными. Если же сила приложена
в одной точке, то она называется сосредоточенной. Реально все силы в природе
являются распределенными, сосредоточенные же силы есть равнодействующие некоторых
распределенных. Например, реакцию рельса, действующую на колесо, иногда представляют
в виде сосредоточенной силы, хотя в действительности колесо и рельс соприкасаются
не в одной точке, а по некоторой площадке. Примерами распределенных сил могут
служить сила тяжести, сила давления воды, давление ветра, сыпучих грузов и т.д.
При решении задач статики часто целесообразно распределенную нагрузку заменять
одной эквивалентной сосредоточенной силой.
Рассмотрим некоторые простейшие примеры распределенных сил, лежащих
в одной плоскости. Плоская система распределенных сил характеризуется ее интенсивностью
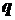 , то есть величиной
силы, приходящейся на единицу длины. Заменим
нагрузку, распределенную вдоль отрезка прямой по произвольному закону, сосредоточенной
силой (рис. 1.2).
, то есть величиной
силы, приходящейся на единицу длины. Заменим
нагрузку, распределенную вдоль отрезка прямой по произвольному закону, сосредоточенной
силой (рис. 1.2).
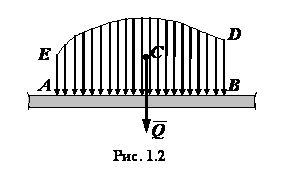 Равнодействующей
распределенной нагрузки будет сила
Равнодействующей
распределенной нагрузки будет сила  , равная по модулю площади
фигуры
, равная по модулю площади
фигуры  , измеряемой в соответствующем
масштабе. Линия действия силы
, измеряемой в соответствующем
масштабе. Линия действия силы 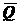 проходит через центр тяжести этой площади.
проходит через центр тяжести этой площади.
В частном случае сил, распределенных вдоль отрезка прямой, значения
эквивалентных сосредоточенных сил могут быть найдены по формулам, определяющим
площади плоских фигур:
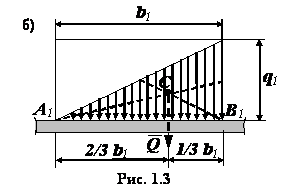
для прямоугольника (рис. 1.3, а)
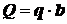 (1.1)
(1.1)

для треугольника (рис.
1.3, б)
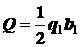 . (1.2)
. (1.2)
Для прямоугольника
линия действия силы 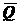 проходит через точку пересечения его диагоналей, а в случае треугольника
через точку пересечения его медиан.
проходит через точку пересечения его диагоналей, а в случае треугольника
через точку пересечения его медиан.
§ 2. Аксиомы статики
твердого тела
В основе статики твердого тела лежат аксиомы, установленные
из опытов и наблюдений. Всё содержание статики может быть получено дедуктивно
(т.е. посредством логических умозаключений с
использованием соответствующего математического аппарата) как следствие этих аксиом.
Аксиома 1 (о равновесии двух сил). Две силы, приложенные
к абсолютно твердому телу, уравновешиваются тогда и только тогда, когда они равны
по величине, противонаправлены и имеют общую линию
действия (рис. 1.4). 
Аксиома 2 (о присоединении и исключении уравновешенных
сил). Действие данной системы сил на твердое тело не изменяется, если к ней
присоединить или исключить из нее уравновешенную систему.
Из аксиом 1 и 2 логически
получаем следствие: не изменяя действия силы на твердое тело,
можно переносить точку приложения силы вдоль линии действия. Иногда этот
факт выражают словами: сила, приложенная к абсолютно твердому телу, есть вектор
скользящий. В самом деле (рис. 1.5), 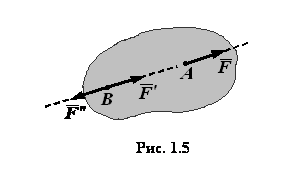 пусть на твердое
тело действует сила
пусть на твердое
тело действует сила  , приложенная в точке
, приложенная в точке
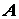 .
Приложим в произвольной точке
.
Приложим в произвольной точке 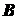 , лежащей на линии действия
силы
, лежащей на линии действия
силы 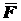 ,
две уравновешенные силы
,
две уравновешенные силы 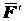 и
и 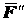 ,
причем
,
причем 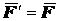 ,
, 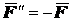 . Согласно аксиоме 2
полученная система из трех сил эквивалентна силе
. Согласно аксиоме 2
полученная система из трех сил эквивалентна силе 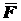 .
Но силы
.
Но силы 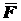 и
и 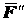 согласно аксиоме 1 уравновешиваются
и их можно отбросить, следовательно, сила
согласно аксиоме 1 уравновешиваются
и их можно отбросить, следовательно, сила 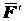 эквивалентна системе
эквивалентна системе
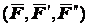 ,
а потому и данной силе
,
а потому и данной силе 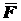 .
.
При формулировании этой аксиомы полагают, что сила при переносе точки
ее приложения работы не совершает.
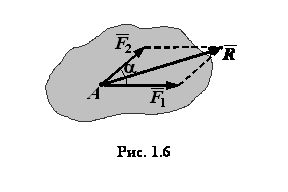 Аксиома 3 (закон параллелограмма). Равнодействующая
двух сил, приложенных к одной точке тела под углом друг к другу, выражается по
величине и по направлению диагональю параллелограмма, построенного на заданных
силах (рис.1.6):
Аксиома 3 (закон параллелограмма). Равнодействующая
двух сил, приложенных к одной точке тела под углом друг к другу, выражается по
величине и по направлению диагональю параллелограмма, построенного на заданных
силах (рис.1.6):
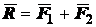 .
.
Величину равнодействующей силы можно определить по теореме косинусов

или по теореме синусов
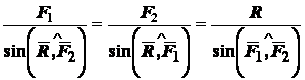 .
.
Аксиома 4 (о действии и противодействии). Два тела
действуют друг на друга с силами, равными по величине и направленными по одной
прямой в противоположные стороны (рис. 1.7). 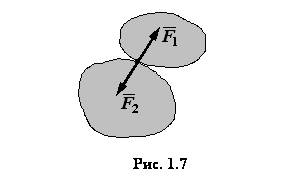
Заметим, что эти силы приложены к
разным телам.
Аксиома 5 (аксиома отвердевания). Равновесие нетвердого
тела не нарушится, если при тех же действующих на него силах оно затвердеет и
станет абсолютно твердым.
На основании этой аксиомы результаты, полученные в статике абсолютно
твердого тела, можно применять к деформируемым телам.
Утверждение, обратное аксиоме 5, неверно (если тело перестает быть
твердым, то его равновесие может нарушиться).
Аксиома 6 (аксиома освобождаемости
от связей). Не изменяя состояния несвободного тела, можно отбросить наложенные
на него связи, приложив их реакции, после чего рассматривать тело как свободное.
§
3. Некоторые виды связей и их реакции
1) Реакция гладкой поверхности
без трения направлена по общей нормали к поверхностям соприкасающихся тел в точке
их касания (рис. 1.8, а, б). Такая реакция называется нормальной. Если
поверхность одного из тел не имеет нормали в точке контакта, реакция при отсутствии
трения направлена по нормали к поверхности другого
(рис. 1.8, в).
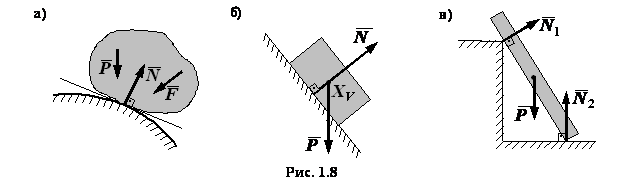
2) Реакция шарнирно-подвижной
опоры без трения направлена перпендикулярно к опорной поверхности (рис. 1.9, а).
3) Реакция шарнирно-неподвижной
опоры без трения проходит через центр шарнира, но направление ее неизвестно.
При решении задач реакцию такой опоры удобно разложить на две составляющие (рис.
1.9, б) или на три, если шарнир пространственный (сферический) (рис. 1.9, в),
направленные параллельно координатным осям. Каждая из этих составляющих считается
неизвестной.
 4) Реакция гибкой нерастяжимой
связи (нити, канаты, цепи) или стержневой связи (прямолинейного стержня, вес
которого не учитывается, с шарнирами на концах) направлена вдоль этой связи (рис.
1.10, а, б).
4) Реакция гибкой нерастяжимой
связи (нити, канаты, цепи) или стержневой связи (прямолинейного стержня, вес
которого не учитывается, с шарнирами на концах) направлена вдоль этой связи (рис.
1.10, а, б).

5) Реакция цилиндрического шарнира (рис. 1.11, а) может иметь любое
направление в плоскости, перпендикулярной к оси шарнира, т.е. в плоскости
 . При решении задач такую реакцию принято
раскладывать на две составляющие
. При решении задач такую реакцию принято
раскладывать на две составляющие  и
и 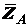 , которые считаются
неизвестными.
, которые считаются
неизвестными.

6) Реакция подпятника (рис, 1.11, б) может иметь любое направление
в пространстве. При решении задач она раскладывается аналогично реакции сферического
шарнира.
7) О реакции жесткой заделки (рис. 1.11, в) будет сказано в § 9.
Г л а в а II
СИСТЕМА СХОДЯЩИХСЯ СИЛ
§ 4. Равнодействующая сходящихся сил
 Если линии действия всех сил системы
Если линии действия всех сил системы 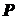 пересекаются в одной точке, то система называется системой сходящихся
сил, а точка пересечения – точкой схода. Пусть к
твердому телу приложена некоторая система сходящихся сил. На основании
следствия из аксиом 1 и 2 можно перенести точки приложения всех сил в точку схода.
Тогда мы получим пучок сил, приложенных в одной точке. Рассмотрим для определенности
пучок трех сил и покажем, что он имеет равнодействующую (рис. 1.12). Для этого
сначала на основании аксиомы параллелограмма определим равнодействующую
пересекаются в одной точке, то система называется системой сходящихся
сил, а точка пересечения – точкой схода. Пусть к
твердому телу приложена некоторая система сходящихся сил. На основании
следствия из аксиом 1 и 2 можно перенести точки приложения всех сил в точку схода.
Тогда мы получим пучок сил, приложенных в одной точке. Рассмотрим для определенности
пучок трех сил и покажем, что он имеет равнодействующую (рис. 1.12). Для этого
сначала на основании аксиомы параллелограмма определим равнодействующую
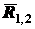 сил
сил 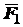 и
и 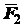 :
: 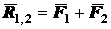 , которая приложена
к точке схода
, которая приложена
к точке схода 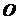 . Далее так же найдем
равнодействующую
. Далее так же найдем
равнодействующую 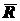 сил
сил 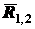 и
и 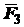 :
:
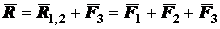 .
.
Аналогично может быть определена равнодействующая
для любого числа сходящихся сил. Следовательно, система сходящихся сил всегда
имеет равнодействующую, равную их векторной сумме и приложенную в точке схода:
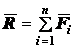 . (1.3)
. (1.3)
Векторная сумма может быть определена или последовательным
применением правила параллелограмма, или,
что проще, построением векторного (силового) многоугольника. Из векторного равенства
(1.3), проектируя его на оси координат, получим:
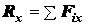 ,
, 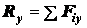 ,
, 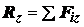 .
.
Модуль равнодействующей определяют
по формуле
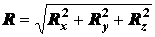 ,
,
а
направляющие косинусы по формулам:
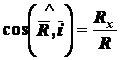 ,
, 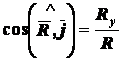 ,
, 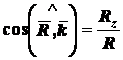 .
.
Для сил, лежащих и одной плоскости,
формулы упрощаются 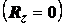 .
.
§ 5. Условие равновесия сходящихся сил
Для сходящихся сил необходимое и достаточное условие равновесия состоит
в равенстве нулю ее равнодействующей. В геометрической форме оно выражается одним
векторным равенством 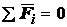 . Это векторное равенство
эквивалентно трем уравнениям равновесия в проекциях на координатные оси:
. Это векторное равенство
эквивалентно трем уравнениям равновесия в проекциях на координатные оси:
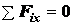 ,
, 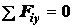 ,
, 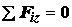 . (1.4)
. (1.4)
Следовательно, для равновесия системы сходящихся сил необходимо
и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из
трёх координатных осей равнялись
нулю.
Для равновесия системы сходящихся сил, лежащих
в одной плоскости, необходимо и достаточно, чтобы выполнялись два уравнения равновесия:
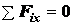 ,
, 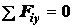 < .
< .
Задача 1.1. Цилиндр весом 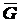 удерживается в равновесии с помощью веревки
удерживается в равновесии с помощью веревки 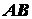 (рис. 1.13). Нормальная
реакция опорной поверхности
(рис. 1.13). Нормальная
реакция опорной поверхности 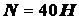 . Определить натяжение
веревки
. Определить натяжение
веревки 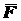 и вес
и вес 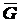 , если известны углы
, если известны углы
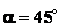 ,
, 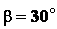 .
. 
Решение. Рассмотрим равновесие системы
сил, приложенных к цилиндру. Освободим цилиндр от связей. Покажем реакции
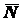 и
и  (нормальная реакция опорной плоскости и натяжение нити). Силы
(нормальная реакция опорной плоскости и натяжение нити). Силы 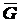 ,
, 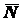 и
и 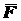 образуют плоскую сходящуюся систему сил. Выбрав координатные оси
образуют плоскую сходящуюся систему сил. Выбрав координатные оси
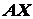 и
и 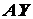 , как показано на схеме,
составляем два уравнения равновесия:
, как показано на схеме,
составляем два уравнения равновесия:
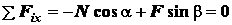 . (а)
. (а)
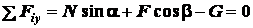 . (б)
. (б)
Из (а) получаем
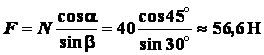 .
.
Из (б)
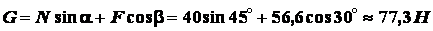 .
.








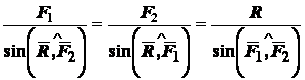 .
.
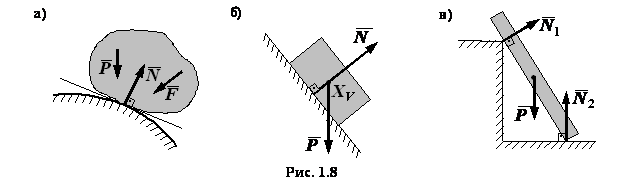




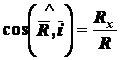 ,
, 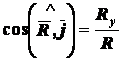 ,
, 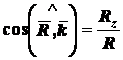 .
.
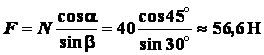 .
.