Г л а в а III

ПЛОСКАЯ СИСТЕМА СИЛ

 

§ 6. Момент силы и пары. Теорема о парах

 

 Система сил, линии действия которых, лежат в одной плос­кости, называется плоской системой сил.

 При изучении плоской системы сил необходимо ввести поня­тия о моменте силы относительно точки, о паре сил и ее моменте.

 Моментом силы относительно точки называется взятое со знаком "плюс" или "минус" произведение модуля силы на ее пле­чо относительно данной точки. Плечом силы относительно точки называется длина перпендикуляра, опущенного из данной точки на линию действия силы. Принято следующее правило знаков: мо­мент силы относительно данной точки положителен, если сила стремится вращать тело вокруг этой точки против часовой стрел­ки, и от­рицателен в противоположном случае. Если линия дейст­вия силы проходит че­рез некоторую точку, то относительно этой точки плечо силы и ее момент равны нулю. Момент силы относительно точки определяется по формуле (рис. 1.14 ):

 

.

 

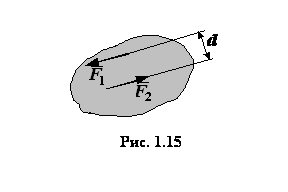
 Парой сил называется совокупность двух равных по модулю, параллель­ных и противонаправленных сил. Расстояние между ли­ниями действия сил пары на­зывается ее плечом. Моментом пары называется взятое со знаком "плюс" или "минус" произведение модуля сил, образующих пару, на ее плечо. Момент пары сил по­ложителен, если пара стремится вращать тело против часовой стрелки, и отрицателен в противоположном случае. Мо­мент пары определяется по формуле (рис. 1.15):

 

,

 

где .

Важнейшее свойство пары сил выражается теоремой об эквивалент­ности пар, которую мы приводим без доказательства: все пары сил, лежащие в одной плоскости и имеющие одинаковые по вели­чине и знаку моменты, эквива­лентны. Из теоремы следует, что действие пары сил на твердое тело полно­стью определяется ее моментом. Не изменяя действие пары на твер­дое тело, мы можем изменять величину, направления и линии действия входящих в нее сил, сохраняя неизменным момент пары. Таким образом, пара сил качественно отличается от простой со­вокупности двух сил, которые, как мы знаем, можно переносить только вдоль линий действия.

 Два других свойства пары сил, необходимые при решении задач:

 алгебраическая сумма проекций обеих сил, составляющих па­ру, на любую ось равна нулю;

 алгебраическая сумма моментов обеих сил, составляющих пару, относи­тельно любой точки в плоскости пары равна моменту самой пары.

 Пользуясь теоремой об эквивалентности пар, можно доказать теорему о сложении пар: любую систему пар, лежащих в одной плоскости, можно заме­нить равнодействующей парой, момент которой равен алгебраической сумме моментов слагаемых пар.

 

§ 7. Приведение плоской системы сил к данному

центру. Теорема Пуансо

 

 Пусть к твердому телу приложена плоская система сил   (рис.1.16). Возьмем в теле произвольную точку , ко­торую будем называть центром приведения, и приложим к ней по­парно уравновешенные силы   и . Заметим, что силы   и образуют при этом пару сил, так что можно считать силу   перенесенной параллельно самой себе в точку   - за­мененной силой   с присоединением пары . Посту­пив так и со всеми оставшимися силами, мы приведем заданную систему сил к совокупности пучка сил , приложенных в точке , и совокупности пар . Сходящиеся силы имеют равнодействующую , приложенную в точке   и равную векторной сумме всех сил системы. Эта сумма называется главным век­тором системы и обозначается .

 Пары можно заменить одной результирующей парой с моментом , равным алгебраической сумме их моментов. Так как момент пары равен сумме момен­тов входящих в нее сил относительно любой точки плоскости пары, то для каж­дой из складываемых пар

 

.

 

Поэтому сумма моментов пар равна сумме моментов самих заданных сил отно­сительно точки , которая называется главным момен­том системы относи­тельно этой точки и обозначается . Та­ким образом, систему сил, произ­вольно расположенных на плоско­сти, можно заменить совокупностью одной силы , равной их главному вектору , и приложенной в произвольно выбран­ном центре приведения, и одной пары, момент которой   равен главному мо­менту   заданных сил относительно центра приве­дения. Это утверждение на­зывается теоремой Пуансо о приведении плоской системы сил к данному цен­тру.

Главный вектор и главный момент системы опре­деляются по формулам:  

 

, . (1.5)

 

§ 8. Равновесие плоской системы сил

 

 Как известно, необходимыми и достаточными условиями рав­новесия пло­ской произвольной системы сил являются равенства нулю ее главного вектора и главного момента.

Существуют три формы уравнений равновесия плоской систе­мы сил. Пер­вую форму получим, спроектировав на оси координат векторное равенство    и присоединив к полу­чившимся двум уравнениям равенство , выражающее условие равенства нулю главного момента:

 

, , . (1.6)

 

 Первые два уравнения называются уравнениями проекций сил на оси координат, третье - уравнением моментов. Точка   может быть выбрана произ­вольно.

 Легко доказать, что необходимые и достаточные условия равновесия пло­ской системы сил могут быть записаны еще в двух формах.

 Вторая форма:

 

, , , (1.7)

 

где ось проекций   должна быть не перпендикулярна к отрезку .

 Третья форма:

 

, , ,  (1.8)

 

где точки   не должны лежать на одной прямой.

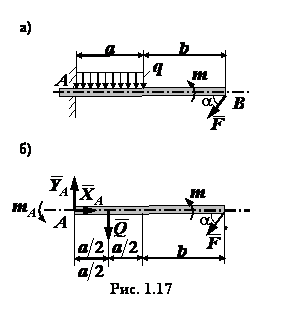
 Отметим, что для любой из трех форм уравнений равновесия число независимых между собой уравнений равновесия равно трем. Задачи, в которых все неизвестные могут быть опреде­лены из уравнений равновесия твердого тела, называются статически оп­реде­ленными. Если же неизвестных больше, чем этих уравнений, то задача оказы­вается статически неопределенной.

Задача 1.2. К балке, жестко заделанной в стену (рис. 1.17, а), при­ложены равно­мерно распределенная нагрузка интенсив­ностью , сосредоточенная сила и пара сил с моментом . Опреде­лить реакцию заделки, если , .

Решение. При жестком защемлении (за­делке) балки в стене на находящийся в стене участок балки действуют неизвест­ные рас­пределенные силы со стороны стены. Так как эти силы образуют плоскую систему, то по теореме Пуансо они экви­валентны одной силе и одной паре. Взяв в качестве центра приведения точку  прило­жим в ней к балке неизвестную по вели­чине и направлению силу в виде сос­тавляющих реакции заделки по осям коор­динат   и . Кроме того, приложим к балке пару с неизвестным моментом . Этот момент назы­вается реактивным моментом за­делки. Таким образом, реакция жесткой заделки характеризуется тремя величи­нами - двумя сос­тав­ляющими реакции заделки   и реактивным моментом , кото­рые необходимо определить. Приложив к балке силы   и   и пару с мо­ментом , на осно­вании аксиомы освобождаемости можем рассматривать ее как сво­бодное твер­дое тело, находящееся в равновесии под действием плоской сис­темы сил - , , ,   и пар сил с моментами ,   (рис. 1.17, б). Здесь   - равнодействующая сосредото­ченная сила, эквивалентная распределенной на­грузке с интенсив­ностью   (см. § 1, рис. 1.3, а).

 

.

 

 Используем первую форму уравнений равновесия:

 

  ,

  ,

 

  .

 При составлении уравнений равновесия учтено, что сумма проекций сил пары на любую ось равна нулю, а сумма моментов сил пары равна моменту са­мой пары. Поэтому в уравнении момен­тов записаны просто моменты прило­женных пар, т.е.   и .

Проверка решения. Для проверки решения сос­тавим выражение суммы мо­ментов относительно какой-либо другой точки, например, точки . При под­становке найденных значений реакций в это выражение оно должно обратиться в нуль:

 

.

 

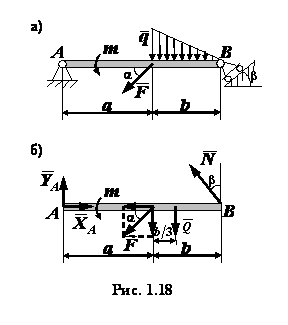
Задача 1.3. Для балки, изображенной вместе с приложенными нагрузками на рис. 1.18, а, определить реакции шарнирно-неподвижной опоры   и шарнирно-

подвижной , если ,

.

Решение. Реакции шарнирно- неподвижной опоры   раз­лагаем на состав­ляющие , . Реакцию шарнирно-подвижной опоры N направляем перпен­дикулярно к опорной поверхности. Состав­ляем уравне­ния равновесия балки как свободного твердого тела, находящегося под дейст­вием заданных сил -   и , пары с момен­том   и реакций , и . Здесь

 

 

(см. § 1, рис. 1.3, б).

 

  , (а)

  ,     (б)

  .   (с)

 

Из (в)

 

.

 

Из (а)

 

.

 

Из (б) 

 

  . 

 

Проверка решения.

 

 

 

§ 9. Равновесие системы твердых тел

  Система твердых тел состоит из нескольких тел, соединён­ных друг с другом шарнирами или соприкасаю­щихся между собой. При решении задач на равновесие системы тел недоста­точно рас­сматривать равновесие всей системы в целом, так как число не­извест­ных может быть больше числа уравнений. Для решения зада­чи необходимо бу­дет дополнительно рассмотреть равновесие ка­кой-нибудь одной или нескольких частей конструкции. Другой способ решения подобных задач со­стоит в том, что конструкцию сразу расчленяют на отдельные тела и состав­ляют уравнения рав­новесия каждого из тел, рассматривая его как свободное. При этом реакции внутренних связей будут попарно равны по модулю и проти­воположны по направлению.

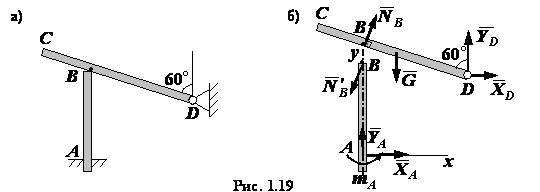
Задача 1.4. Однородный стержень   весом   опирается на вертикаль­ную стойку . Определить реакции шарнирной опоры , заделки   и силу

взаимодействия балок   и , если размеры .

Решение. Система твердых тел состоит из двух балок (рис. 1.19, а). Рассмот­рим равновесие каждой из балок отдельно.

 

 

Отбра­сываем связи, заменяя их дей­ствие реакциями. На балку  действуют силы (рис. 1.19, б):  - вес балки (задаваемая сила),   и   - составляющие реакции шарнира ;   - реакция балки . На балку   действуют силы: , ,   и  (реакция балки ). По аксиоме о действии и противодействии: . Выбираем оси координат с началом в точке .

 Составим уравнения равновесия.

 Для балки :

 

, (I)

, (II)

  . (III)

 

 Для балки :

 

, (IV)

, (V)

  . (VI)

 Из (I) находим

 

.

 

 Из (II)

 

.

 

 Из (III)

 

.

 

 Из (IV)

 

.

 

 Из (V)    .

 

 Из (VI)
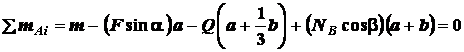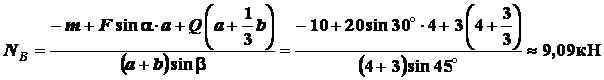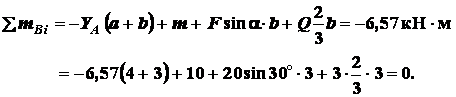
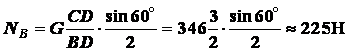