§ 10. Расчет усилий в стержнях ферм
Фермой называется неизменяемая стержневая система, состоящая
из прямолинейных стержней, соединённых между собой на концах посредством
шарниров. Шарниры, соединяющие
стержни, называются узлами фермы. Слово "неизменяемая" означает,
что взаимное расположение стержней остается неизменным. Ограничимся рассмотрением
жестких плоских ферм без лишних стержней, образованных из треугольников. В таких
фермах число стержней 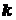 и число узлов
и число узлов 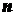 связаны соотношением
связаны соотношением
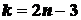 .
.
При расчете усилий в стержнях фермы предполагают, что вес стержней
пренебрежимо мал в сравнении с действующими на ферму силами и что эти силы приложены
к ней только в узлах. При этих допущениях стержни фермы являются стержневыми
связями для ее узлов. Реакции стержневых связей направляют вдоль стержней, предполагая,
что они растянуты (от узлов). Для сжатых стержней в результате решения уравнений
равновесия будем получать отрицательные значения реакций.
Для расчета усилий в стержнях нужно сначала определить внешние опорные
реакции. Усилия в стержнях могут быть определены двумя методами - методом вырезания
узлов и методом сквозных сечений. При первом методе последовательно рассматривают
равновесие узлов фермы, выбирая каждый раз такой узел, где сходится не более двух
стержней, усилия в которых неизвестны. Для каждого узла составляют по два уравнения
равновесия и из них определяют реакции стержней. При втором методе ферму мысленно
рассекают на две части так, чтобы в сечение попало
не более трёх стержней, усилия в которых
неизвестны, и для одной из двух частей составляют три уравнения равновесия плоской
системы сил. Уравнения необходимо составить так, чтобы в каждом уравнении была
только одна неизвестная реакция стержня (метод Риттера).
Задача
1.5. Определить
усилия во всех стержнях фермы, показанной вместе с приложенными силами на рис.
1.20, если 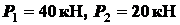 .
.

Решение. Рассматривал ферму как одно
твердое тело, составляем уравнения равновесия приложенной к ней плоской системы
внешних сил - заданных 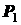 и
и 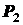 и реакций внешних связей
и реакций внешних связей 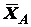 ,
, 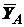 ,
, 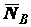 .
Используем первую форму уравнений равновесия плоской системы сил:
.
Используем первую форму уравнений равновесия плоской системы сил:
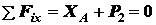 ,
, 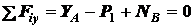 ,
, 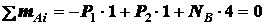 .
.
Из
этих уравнений находим
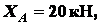
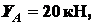
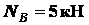 .
.
 Покажем применение метода вырезания узлов.
Покажем применение метода вырезания узлов.
Вырежем узел 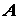 .
Для этого освобождаем его от связей - внешней (шарнирно-неподвижной опоры) и
внутренней (стержней 1 и 2), приложив реакции опоры
.
Для этого освобождаем его от связей - внешней (шарнирно-неподвижной опоры) и
внутренней (стержней 1 и 2), приложив реакции опоры 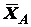 ,
, 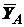 и стержней
и стержней 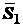 ,
, 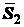 (рис. 1.21). Составляем два уравнения равновесия плоской системы сходящихся
сил, приложенных и точке
(рис. 1.21). Составляем два уравнения равновесия плоской системы сходящихся
сил, приложенных и точке 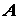 :
:
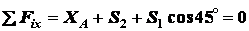 ,
, 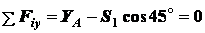 .
.
Из них находим:
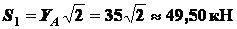 ,
,
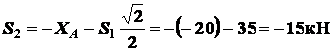 .
.
Стержень 1 растянут, стержень
2 сжат.
 Далее вырезаем узел
Далее вырезаем узел 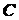 , так как для него неизвестны
усилия лишь в двух cтержнях (3 и 4). Схема приложения
сил показана на рис. 1.22. Реакция стержня 2 на узел
, так как для него неизвестны
усилия лишь в двух cтержнях (3 и 4). Схема приложения
сил показана на рис. 1.22. Реакция стержня 2 на узел 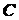 обозначена
обозначена 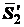 . Она также направлена от узла в сторону
стержня, т.е. противоположно реакции
. Она также направлена от узла в сторону
стержня, т.е. противоположно реакции 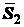 стержня 2 на узел
стержня 2 на узел 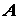 , и равна ей как по величине,
так и по знаку:
, и равна ей как по величине,
так и по знаку: 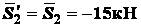 .
.
Уравнения равновесия узла 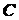 имеют вид
имеют вид
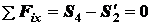 ,
,
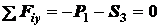 .
.
Из этих уравнений определяем
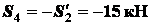 ,
,
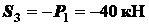 .
.
Оба стержня сжаты. Для дальнейшего расчета усилий
в стержнях методом вырезания узлов можно последовательно вырезать узлы 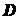 ,
, 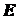 и
и 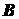 . Студентам рекомендуется
проделать это самостоятельно.
. Студентам рекомендуется
проделать это самостоятельно.
(Ответы:
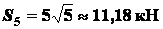 ;
;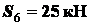 ;
; 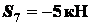 ;
;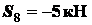 ;
; 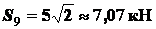 ).
).
Покажем применение метода сквозных сечений.
 Рассекаем ферму по стержням 4, 5, 6 на две части, правую часть мысленно
отбрасываем, а к левой прикладываем реакции перерезаемых стержней
Рассекаем ферму по стержням 4, 5, 6 на две части, правую часть мысленно
отбрасываем, а к левой прикладываем реакции перерезаемых стержней 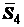 ,
, 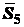 ,
, 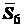 (рис. 1.23). Для левой части фермы составляем уравнения равновесия:
(рис. 1.23). Для левой части фермы составляем уравнения равновесия:
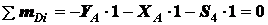 ;
;
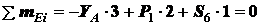 ;
;
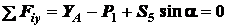 ;
;
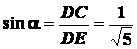 .
.
Точки 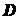 и
и 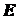 выбраны в качестве центров моментов потому, что в каждой из них пересекаются
линии действия двух неизвестных сил, а ось
выбраны в качестве центров моментов потому, что в каждой из них пересекаются
линии действия двух неизвестных сил, а ось 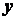 - в качестве оси проекций потому, что к ней две неизвестные силы перпендикулярны.
Заметим, что ось
- в качестве оси проекций потому, что к ней две неизвестные силы перпендикулярны.
Заметим, что ось 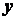 не перпендикулярна отрезку
не перпендикулярна отрезку 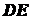 (вторая форма уравнений равновесия). В результате мы составили 3 уравнения,
в каждом из которых по одной неизвестной. Из этих уравнений получили те же значения
реакций:
(вторая форма уравнений равновесия). В результате мы составили 3 уравнения,
в каждом из которых по одной неизвестной. Из этих уравнений получили те же значения
реакций:
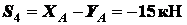 ,
,
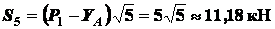 ,
,
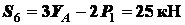 .
.
Г л а в а IV
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
§ 11. Момент силы относительно точки
как
вектор
В случае плоской системы сил момент силы относительно точки был определен
как алгебраическая величина. При пространственном расположении сил этого определения
недостаточно, так как плоскости, проходящие
через линии действия сил и точку, относительно которой определяется момент,
различны. Поэтому момент силы относительно точки в пространстве определим
как векторную величину в виде векторного произведения 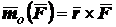 , где
, где 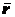 - радиус-вектор, проведённый из точки
- радиус-вектор, проведённый из точки 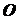 в точку приложения
в точку приложения 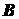 силы
силы 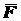 (рис. 1.24). Итак, вектор
(рис. 1.24). Итак, вектор 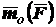 направлен перпендикулярно к плоскости, содержащей линию действия силы
и точку
направлен перпендикулярно к плоскости, содержащей линию действия силы
и точку 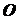 , так что с его конца
вращение силы вокруг точки видно происходящим против часовой стрелки. Модуль
вектора
, так что с его конца
вращение силы вокруг точки видно происходящим против часовой стрелки. Модуль
вектора 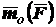 равен произведению модуля силы на расстояние от данной точки до линии действия
силы (плечо силы), т.е.
равен произведению модуля силы на расстояние от данной точки до линии действия
силы (плечо силы), т.е.
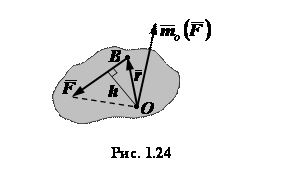
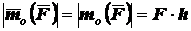 .
.
§ 12. Момент силы
относительно оси
Моментом силы 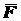 относительно оси
относительно оси
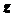 (рис. 1.25), называется алгебраическая величина, абсолютное значение
которой равняется произведению модуля проекции силы
(рис. 1.25), называется алгебраическая величина, абсолютное значение
которой равняется произведению модуля проекции силы 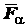 на плоскость
на плоскость 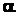 , перпендикулярную к
оси
, перпендикулярную к
оси 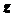 , на расстояние
, на расстояние
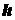 от точки
от точки 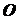 пересечения оси с этой
плоскостью до линии действия проекции силы
на плоскость
пересечения оси с этой
плоскостью до линии действия проекции силы
на плоскость 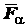 , т.е.
, т.е.
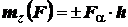 .
.
 Знак "плюс'' - если
направление вращения силы
Знак "плюс'' - если
направление вращения силы 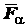 вокруг точки
вокруг точки 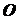 с конца оси
с конца оси 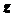 видно происходящим против часовой стрелки, если по часовой стрелке, то
знак "минус''. Очевидно, что момент силы относительно
оси равен нулю, если линия действия силы и ось лежат в одной плоскости.
видно происходящим против часовой стрелки, если по часовой стрелке, то
знак "минус''. Очевидно, что момент силы относительно
оси равен нулю, если линия действия силы и ось лежат в одной плоскости.
В случае пространственной системы сил главным моментом относительно
точки называется векторная сумма моментов всех сил системы относительно той
же точки:
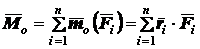 .
.
Главным моментом пространственной системы сил относительно оси
называется сумма моментов всех сил системы относительно этой оси:

Зная
главные моменты системы сил относительно осей декартовых координат, можно вычислить
модуль главного момента относительно начала координат 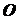 и его направляющие косинусы
и его направляющие косинусы
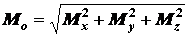 ,
,
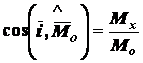 ;
;
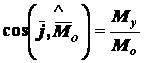 ;
;
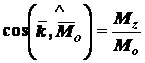 .
.
§ 13.
Равновесие твердого тела под действием произвольной пространственной системы сил
Для равновесия твердого тела под действием произвольной пространственной
системы сил необходимо и достаточно, чтобы суммы проекций всех слагаемых сил
на произвольно выбранные оси декартовых координат 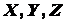 и суммы моментов всех сил относительно этих осей равнялись нулю:
и суммы моментов всех сил относительно этих осей равнялись нулю:
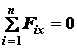 ;
; 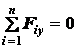 ;
; 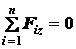 ;
;
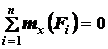 ;
; 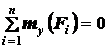 ;
; 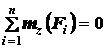 .
.
В случае произвольной пространственной
системы сил задача является статически определенной, если число алгебраических
неизвестных не более шести.
Задача 1.6. Определить
реакции подшипников вала червячного редуктора и момент пары  , если на
червяк действует силы:
, если на
червяк действует силы: 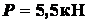 ,
, 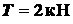 ,
, 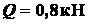 ;
;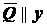 ,
, 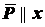 . Размеры:
. Размеры: 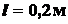 ,
, 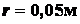 .
.
Решение. Рассмотрим
равновесие вала (рис. 1.26). Освободим вал от связей и приложим к нему реакции
связей. На рис. 1.26: 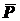 ,
, 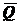 ,
, 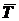 - активные силы;
- активные силы;  -момент пары сил;
-момент пары сил; 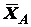 ,
, 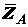 - составляющие реакции подшипника
- составляющие реакции подшипника 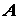 ;
; 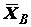 ,
, 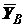 ,
, 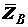 - составляющие реакции упорного подшипника (подпятника)
- составляющие реакции упорного подшипника (подпятника) 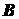 . Имеем шесть неизвестных
величин -
. Имеем шесть неизвестных
величин - 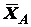 ,
, 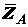 ,
, 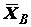 ,
, 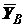 ,
, 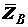 и
и  .
.
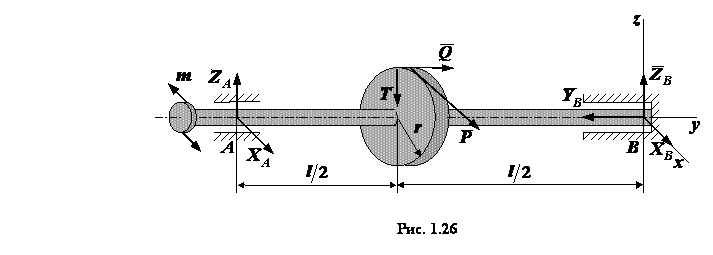
Составим шесть уравнений равновесия:
 ; (а)
; (а) 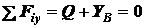 ; (б)
; (б)
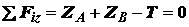 ; (в)
; (в)
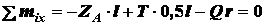 ;
(г)
;
(г)
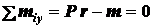 ; (д)
; (д)
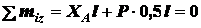 . (е)
. (е)
Из (б), (д) и (е)
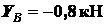 ;
; 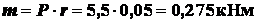 ;
; 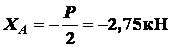 .
.
Зная 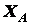 , из (а) получаем
, из (а) получаем
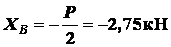 .
.
Из
(г)
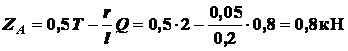 .
.
Подставляя 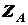 в (в), находим
в (в), находим
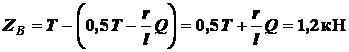 .
.