Г л а в а VI
ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
§ 18. Центр параллельных сил
Пусть дана система параллельных сил
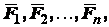 приложенных в точках
приложенных в точках
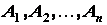 и направленных в одну сторону (рис. 1.32). Такая система сил может
быть приведена к равнодействующей
и направленных в одну сторону (рис. 1.32). Такая система сил может
быть приведена к равнодействующей 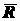 , параллельной заданным
силам и направленной в ту же сторону. Так как сила, приложенная к абсолютно твердому
телу, есть вектор скользящий, то равнодействующую
, параллельной заданным
силам и направленной в ту же сторону. Так как сила, приложенная к абсолютно твердому
телу, есть вектор скользящий, то равнодействующую 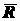 можно приложить в любой точке
можно приложить в любой точке 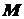 на линии ее действия. Выведем уравнение линии действия равнодействующей
параллельных сил.
на линии ее действия. Выведем уравнение линии действия равнодействующей
параллельных сил.
 Согласно теореме
Вариньона момент равнодействующей относительно каждой оси равен алгебраической
сумме моментов составляющих относительно этой же оси. Поэтому, используя аналитические
выражения для моментов силы относительно координатных осей, можно написать:
Согласно теореме
Вариньона момент равнодействующей относительно каждой оси равен алгебраической
сумме моментов составляющих относительно этой же оси. Поэтому, используя аналитические
выражения для моментов силы относительно координатных осей, можно написать:
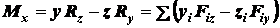 ; (1.9)
; (1.9)
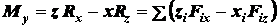 , (1.10)
, (1.10)
где 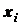 ,
, 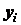 и
и 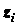 - координаты точки приложения силы
- координаты точки приложения силы 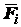 ;
;
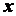 ,
, 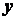 и
и 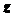 - координаты точки
- координаты точки 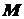 (рис. 1.32).
(рис. 1.32).
Обозначим углы, образуемые направлением сил с
координатными осями 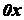 ,
, 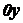 и
и 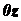 через
через 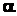 ,
, 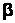 и
и 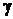 . Тогда проекции на оси
координат заданных сил и их равнодействующей
. Тогда проекции на оси
координат заданных сил и их равнодействующей 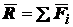 будут равны:
будут равны:
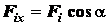 ;
;
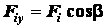 ;
;
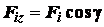 ;
;
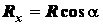 ;
;
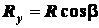 ;
;
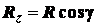 .
.
Подставляя эти выражения
в равенства (1.9) и (1.10), после некоторых преобразований получим
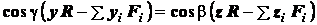 ;
(1.11)
;
(1.11)
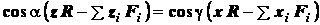 .
(1.12)
.
(1.12)
Разделив равенство (1.11) на 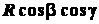 , а (1.12) – на
, а (1.12) – на 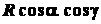 и заменив
и заменив 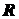 на
на 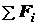 , получим
, получим
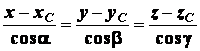 , (1.13)
, (1.13)
где
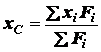 ;
;
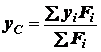 ;
;
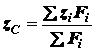 . (1.14)
. (1.14)
Мы получили уравнение
линии действия равнодействующей 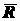 заданных сил. Оно показывает, что линия действия равнодействующей
заданных сил. Оно показывает, что линия действия равнодействующей 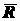 при любых значениях
при любых значениях 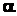 ,
, 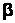 и
и 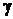 проходит через точку
проходит через точку 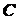 с координатами
с координатами 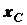 ,
, 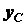 ,
, 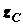 , вычисляемыми по формулам
(1.14).
, вычисляемыми по формулам
(1.14).
Это
значит, что если все заданные силы повернуть вокруг точек их приложения на один
и тот же угол и в одну и ту же сторону, то линия действия равнодействующей, повернувшись
на тот же угол, по-прежнему будет проходить через точку 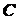 (рис. 1.33).
(рис. 1.33).
Точка 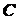 называется центром системы параллельных сил. Положение центра параллельных
сил не зависит от направления сил, а определяется только их величинами и точками
приложения.
называется центром системы параллельных сил. Положение центра параллельных
сил не зависит от направления сил, а определяется только их величинами и точками
приложения.  Центр параллельных
сил есть точка, через которую проходит линия равнодействующей системы параллельных
сил, приложенных в заданных точках, при любом изменении направления этих сил
в пространстве.
Центр параллельных
сил есть точка, через которую проходит линия равнодействующей системы параллельных
сил, приложенных в заданных точках, при любом изменении направления этих сил
в пространстве.
Изложенные рассуждения и результаты будут верными
и в случае системы параллельных сил, имеющих равнодействующую, но не направленных
в одну сторону. В этом случае нужно только во всех формулах брать значения 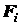 со знаком «плюс», если
со знаком «плюс», если 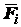 направлена в ту же сторону, что и
направлена в ту же сторону, что и 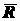 , и со знаком «минус»
в противоположном случае.
, и со знаком «минус»
в противоположном случае.
Три формулы (1.14) можно заменить одной векторной
формулой
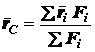 , (1.15)
, (1.15)
где 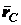 и
и 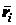 - радиус-векторы точки
- радиус-векторы точки  и точек приложения заданных параллельных сил, проведенные из начала координат
и точек приложения заданных параллельных сил, проведенные из начала координат
 .
.
Действительно, проекции радиус-вектора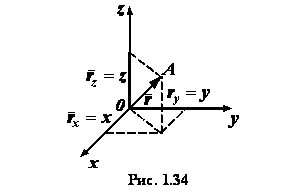
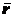 любой точки
любой точки 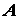 на оси
на оси 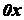 ,
, 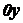 и
и 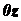 равны соответствующим координатам точки
равны соответствующим координатам точки 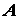 (рис. 1.34). Поэтому, проектируя векторное равенство (1.15) на оси координат,
получим формулы (1.14), определяющие координаты центра параллельных сил.
(рис. 1.34). Поэтому, проектируя векторное равенство (1.15) на оси координат,
получим формулы (1.14), определяющие координаты центра параллельных сил.
§ 19. Понятие о центре тяжести
твердого тела
Если размеры тела малы по сравнению
с радиусом Земли, то можно считать, что силы тяжести всех частиц тела образуют
систему параллельных сил. Их равнодействующая называется силой тяжести,
а центр этих параллельных сил – центром тяжести тела.
Центр тяжести – это точка, через которую
при любом положении тела проходит линия действия его силы тяжести. Координаты
центра тяжести тела могут быть определены по формулам (1.14):
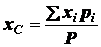 ;
;
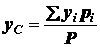 ;
;
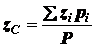 . (1.16)
. (1.16)
Здесь
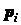 ,
, 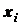 ,
, 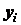 ,
, 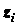 - вес и координаты
- вес и координаты 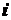 - й частицы тела;
- й частицы тела;
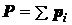 - вес тела.
- вес тела.
Если тело однородное, то вес 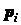 любой частицы тела пропорционален ее объему
любой частицы тела пропорционален ее объему 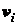 . Поэтому координаты
центра тяжести такого тела будут равны:
. Поэтому координаты
центра тяжести такого тела будут равны:
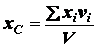 ;
;
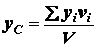 ;
;
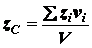 , (1.17)
, (1.17)
где 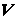 - объем тела.
- объем тела.
Если однородное тело имеет форму тонкой оболочки
постоянной толщины, то его можно рассматривать как материальную поверхность.
Вес 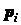 каждой элементарной площадки такой поверхности пропорционален величине площади
каждой элементарной площадки такой поверхности пропорционален величине площади 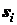 этого элемента. Для координат центра тяжести поверхности получаем
этого элемента. Для координат центра тяжести поверхности получаем
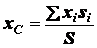 ;
;
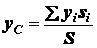 ;
;
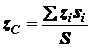 , (1.18)
, (1.18)
где 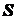 - площадь поверхности.
- площадь поверхности.
В случае плоской фигуры, лежащей в плоскости
 , необходимо вычислить
с помощью (1.18) только координаты
, необходимо вычислить
с помощью (1.18) только координаты 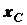 и
и 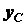 .
.
Суммы
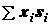 и
и 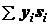 называются статическими
моментами площадисоответственно относительно осей
называются статическими
моментами площадисоответственно относительно осей 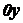 и
и 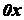 .
.
Тело, у которого одно из измерений очень велико
по сравнению с другими (например, длинная трубка, проволока и т.п.), можно рассматривать
как материальную линию. Вес каждого элемента однородной материальной линии
пропорционален длине 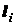 элемента. В этом случае общие формулы (1.16) примут вид
элемента. В этом случае общие формулы (1.16) примут вид
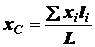 ;
;
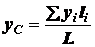 ;
;
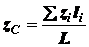 , (1.19)
, (1.19)
Формулы (1.16) – (1.19) являются точными, строго
говоря, лишь при разбиении тело на бесконечное число бесконечно малых частиц.
Если же число частиц, на которые мысленно
разбито тело, конечное, то в общем случае эти формулы будут приближенными, так
как координаты 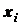 ,
, 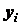 и
и 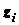 при этом могут быть определены лишь с точностью до размеров частиц. Чем
меньше эти частицы, тем меньше будет ошибка, которую мы сделаем при вычислении
координат центра тяжести. К точным выражениям можно прийти лишь в результате
предельного перехода, когда размер каждой частицы стремится к нулю, а число их
неограниченно возрастает. Как известно, такой предел называется определенным
интегралом. Поэтому фактическое определение координат центров тяжести тел по формулам
(1.16)—(1.19) в общем случае требует замены сумм соответствующими им интегралами
и применения методов интегрального исчисления. Однако в некоторых частных случаях
оказывается возможным обойтись и элементарными приемами, которые мы рассмотрим
ниже.
при этом могут быть определены лишь с точностью до размеров частиц. Чем
меньше эти частицы, тем меньше будет ошибка, которую мы сделаем при вычислении
координат центра тяжести. К точным выражениям можно прийти лишь в результате
предельного перехода, когда размер каждой частицы стремится к нулю, а число их
неограниченно возрастает. Как известно, такой предел называется определенным
интегралом. Поэтому фактическое определение координат центров тяжести тел по формулам
(1.16)—(1.19) в общем случае требует замены сумм соответствующими им интегралами
и применения методов интегрального исчисления. Однако в некоторых частных случаях
оказывается возможным обойтись и элементарными приемами, которые мы рассмотрим
ниже.
§ 20.
Некоторые приемы определения координат
центра тяжести
Метод симметрии. Если однородное
тело имеет плоскость, ось или центр симметрии, то центр тяжести тела лежит соответственно
в этой плоскости, на этой оси или в этом центре. Например, центр тяжести
однородного круглого конуса лежит на его оси, а центр тяжести однородного шара
— в его центре.
Метод группировки. Если тело можно разбить на конечное число таких частей, для каждой
из которых положение центра тяжести известно, то координаты центра тяжести тела
могут быть определены, и притом точно, непосредственно по общим формулам (1.16)
— (1.19), если рассматривать в них 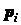 (или
(или 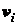 ,
, 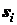 ,
, 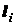 ) и
) и 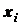 ,
, 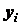 ,
, 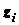 как соответственно вес (или объем, площадь, длину) и координаты центров
тяжести частей тела.
как соответственно вес (или объем, площадь, длину) и координаты центров
тяжести частей тела.
Эти утверждения могут быть доказаны с помощью формул (1.16).
Докажем, например, второе из них. Пусть тело можно разбить
на 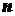 частей, для каждой из которых известны вес
частей, для каждой из которых известны вес 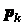 и координаты
и координаты 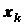 ,
, 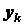 ,
, 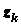 центра тяжести
центра тяжести 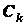 ,
, 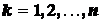 . Разобьем каждую из
сумм
. Разобьем каждую из
сумм 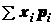 ,
, 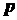 ,
, 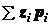 в формулах (1.16) на
в формулах (1.16) на 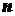 слагаемых, каждое из которых распространено только на одну из частей, на
которые разбито тело. Например,
слагаемых, каждое из которых распространено только на одну из частей, на
которые разбито тело. Например,
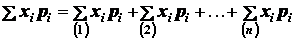 .
.
Но согласно первой формуле (1.16)
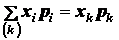 ,
,
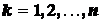 ;
;
тогда
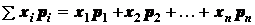 .
.
Это равенство будет совершенно точным при переходе в левой
части к пределу (определенному интегралу); при этом правая часть выражается конечным
числом слагаемых. Поэтому получаем (точно)
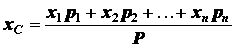
и
т.д., что и доказывает наше утверждение.
Задача 1.9. Определить положение центра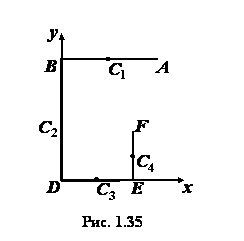 тяжести
плоской фигуры
тяжести
плоской фигуры 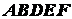 (рис. 1.35), изогнутой из тонкой проволоки. Даны размеры:
(рис. 1.35), изогнутой из тонкой проволоки. Даны размеры: 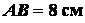 ,
, 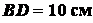 ,
, 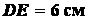 ,
, 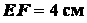 .
.
Решение. Фигура состоит из четырех отрезков:
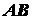 ,
, 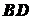 ,
, 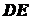 и
и 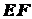 . На эти четыре части
и разбиваем фигуру. Середины этих отрезков являются центрами симметрии, а, следовательно,
и центрами тяжести (точки
. На эти четыре части
и разбиваем фигуру. Середины этих отрезков являются центрами симметрии, а, следовательно,
и центрами тяжести (точки 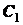 ,
, 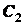 ,
, 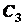 и
и 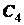 на рис. 1.35).
на рис. 1.35).
Исходя из размеров отрезков, находим координаты центров
тяжести отрезков 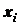 и
и 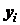 и длину
и длину 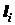 :
:
для отрезка 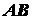
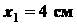 ;
;
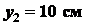 ;
;
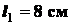 ,
,
для отрезка 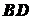
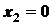 ;
;
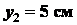 ;
;
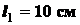 ,
,
для отрезка 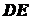
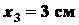 ;
;
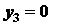 ;
;
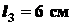 ,
,
для отрезка 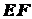
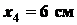 ;
;
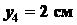 ;
;
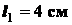 .
.
Тогда по формулам (1.19):
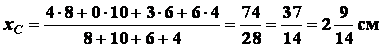 ;
;
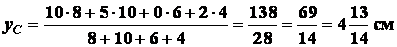 .
.
 Задача 1.10. Определить координаты центра тяжести однородной
пластинки, изображенной на рис. 1.36, зная, что
Задача 1.10. Определить координаты центра тяжести однородной
пластинки, изображенной на рис. 1.36, зная, что 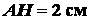 ,
, 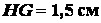 ,
, 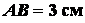 ,
, 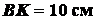 ,
, 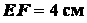 ,
, 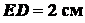 .
.
Решение. Проводим оси
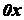 и
и 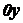 и разбиваем пластину на три прямоугольника:
и разбиваем пластину на три прямоугольника: 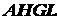 ,
, 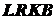 и
и 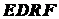 (линии разреза показаны на рис. 1.36). Вычисляем координаты центров тяжести
каждого из прямоугольников и их площади:
(линии разреза показаны на рис. 1.36). Вычисляем координаты центров тяжести
каждого из прямоугольников и их площади:
Для
прямоугольника 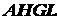
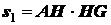 ;
;
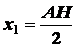 ;
;
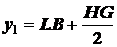 .
.
Так как 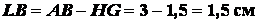 , то
, то
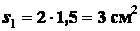 ;
;
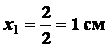 ;
;
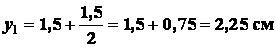 .
.
Для
прямоугольника 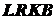
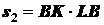 ;
;
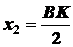 ;
; 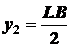 ,
,
т.е.
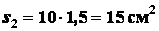 ;
;
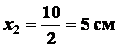 ;
;
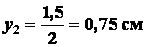 .
.
Для прямоугольника
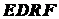
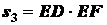 ;
;
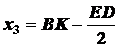 ;
;
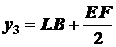 ,
,
т.е.
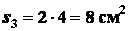 ;
;
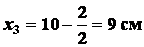 ;
;
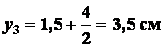 .
.
По
формулам (1.18) получаем:
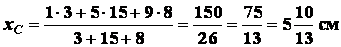 ;
;
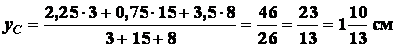 .
.
Метод
дополнения, или отрицательных весов, является частным
случаем метода группировки. Его сущность
ясна из следующего примера.
Задача 1.11. В однородной квадратной пла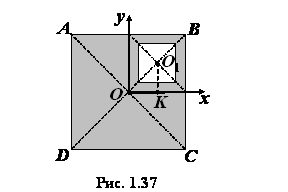 стинке
стинке  со стороной
со стороной 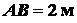 вырезано отверстие в виде квадрата, стороны которого
параллельны сторонам пластины и равны
вырезано отверстие в виде квадрата, стороны которого
параллельны сторонам пластины и равны 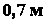 . Определить координаты
центра тяжести оставшейся части пластинки, зная, что
. Определить координаты
центра тяжести оставшейся части пластинки, зная, что 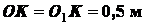 , где
, где 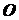 и
и 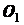 - центры квадратов (рис. 1.37).
- центры квадратов (рис. 1.37).
Решение. Будем рассматривать данную пластинку
как совокупность полного квадрата 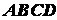 без выреза и квадрата с центром в точке
без выреза и квадрата с центром в точке 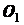 с отрицательной площадью (отрицательным весом),
наложенного на место выреза. В формулах для координат центров тяжести (1.19) отрицательные
площади (веса) должны учитываться со знаком «минус».
с отрицательной площадью (отрицательным весом),
наложенного на место выреза. В формулах для координат центров тяжести (1.19) отрицательные
площади (веса) должны учитываться со знаком «минус».
Через центр квадрата проводим оси
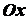 и
и 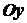 . В
выбранной системе координат центры тяжести квадратов совпадают с точками
. В
выбранной системе координат центры тяжести квадратов совпадают с точками
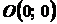 и
и 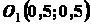 .
Найдем площади квадратов:
.
Найдем площади квадратов:
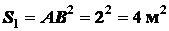 ;
; 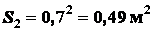 .
.
На основании
первых двух формул (1.18) получим
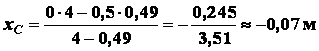 ,
,
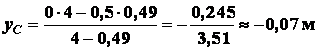 .
.
Теоремы Паппа—Гульдина. Во многих случаях определение координат центра тяжести плоских фигур и
линий упрощается применением теорем Паппа - Гульдина.
Первая теорема. Объем тела, образованного вращением фигуры вокруг оси, лежащей с ней
в одной плоскости и ее не пересекающей, равен произведению площади фигуры на длину
окружности, описанной ее центром тяжести.
 Доказательство. Объем тела, которое образуется
при вращении плоской фигуры
Доказательство. Объем тела, которое образуется
при вращении плоской фигуры 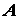 (рис. 1.38) вокруг оси
(рис. 1.38) вокруг оси 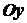 , можно вычислить как
сумму объемов тел, образуемых вращением элементарных площадок
, можно вычислить как
сумму объемов тел, образуемых вращением элементарных площадок 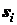 . Объем каждого такого
бесконечно малого тела и всего тела
. Объем каждого такого
бесконечно малого тела и всего тела
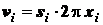 ;
;
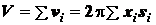 .
.
На основании формул (1.17) имеем
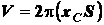 , (1.20)
, (1.20)
где 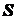 - площадь фигуры;
- площадь фигуры;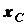 - координата ее центра
тяжести.
- координата ее центра
тяжести.
Приравняв правые части последних формул,
устанавливаем справедливость первой теоремы Папа-Гульдена.
Вторая теорема. Боковая повер хность тела, образованного вращением плоской линии вокруг оси, лежащей с ней в
одной плоскости и ее не пересекающей равна произведению длины линии на длину
окружности, описанной ее центром тяжести.
хность тела, образованного вращением плоской линии вокруг оси, лежащей с ней в
одной плоскости и ее не пересекающей равна произведению длины линии на длину
окружности, описанной ее центром тяжести.
Доказательство. Боковая поверхность 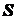 тела, образованного вращением дуги вокруг оси
тела, образованного вращением дуги вокруг оси 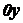 , лежащей с ней в одной
плоскости, равна сумме поверхностей, описанных элементарными дугами
, лежащей с ней в одной
плоскости, равна сумме поверхностей, описанных элементарными дугами 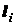 (см. рис. 1.39):
(см. рис. 1.39):
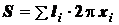 .
.
С помощью формул (1.18) имеем
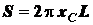 , (1.21)
, (1.21)
где 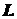 - длина линии;
- длина линии;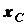 - координата
ее центра тяжести.
- координата
ее центра тяжести.
Приравняв правые части последних формул,
устанавливаем справедливость второй теоремы Папа-Гульдена.
Задача 1.12. Определить положение центра тяжести
площади равнобедренного прямоугольного треугольника 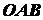 с катетами
с катетами 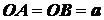 (рис. 1.40).
(рис. 1.40).
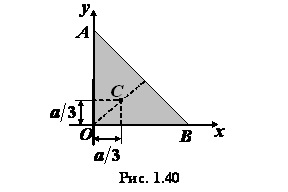 Решение. Через вершину прямого угла заданного
треугольника проводим оси
Решение. Через вершину прямого угла заданного
треугольника проводим оси  и
и  . Вращая
треугольник вокруг оси
. Вращая
треугольник вокруг оси  , получим конус с радиусом
основания
, получим конус с радиусом
основания 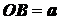 и высотой
и высотой 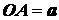 (см. рис. 1.40). Объем этого конуса и
площадь заданного треугольника
(см. рис. 1.40). Объем этого конуса и
площадь заданного треугольника
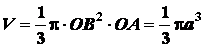 ,
,
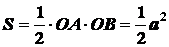 .
.
Поэтому на основании первой теоремы Паппа—Гульдина
уравнение (1.20) (координата 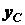 при таком вращении не меняется) принимает вид
при таком вращении не меняется) принимает вид
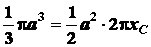 или
или 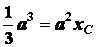 ,
,
откуда
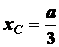 .
.
При вращении треугольника  вокруг оси получаем
вокруг оси получаем
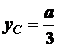 .
.
Задача 1.13. Определить положение центра  тяжести дуги полуокружности радиуса
тяжести дуги полуокружности радиуса 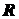 (рис. 1.41).
(рис. 1.41).
Решение. Так как ось симметрии полуокружности
совпадает с осью 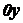 , то центр тяжести находится
на этой оси, т.е.
, то центр тяжести находится
на этой оси, т.е. 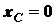 .
.
Найдем координату 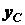 . Вращая полуокружность вокруг оси
. Вращая полуокружность вокруг оси 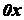 , получим сферу (см.
рис. 1.41). Площадь сферы равна
, получим сферу (см.
рис. 1.41). Площадь сферы равна 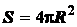 , а длина полуокружности
-
, а длина полуокружности
- 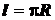 . На основании второй
теоремы Паппа - Гульдина имеем
. На основании второй
теоремы Паппа - Гульдина имеем
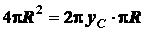 ,
,
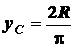 .
.
§ 21. Центры тяжести некоторых однородных линий,
плоских
фигур и тел
Центр тяжести площади треугольника. Разобьем площадь треугольника  на бесконечно тонкие элементарные полоски, параллельные основанию
на бесконечно тонкие элементарные полоски, параллельные основанию
 (рис. 1.42). Центр тяжести каждой такой полоски расположен в ее середине.
Геометрическое место центров
(рис. 1.42). Центр тяжести каждой такой полоски расположен в ее середине.
Геометрическое место центров 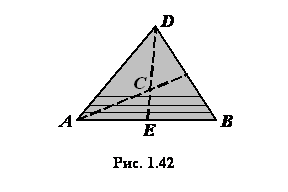 тяжести всех полосок есть медиана
тяжести всех полосок есть медиана  . На ней
поэтому и должен лежать центр тяжести всего треугольника. Так как такое же рассуждение
справедливо и для двух других медиан, то центр тяжести треугольника лежит
в точке пересечения его медиан. При задании вершин треугольника их координатами
получим
. На ней
поэтому и должен лежать центр тяжести всего треугольника. Так как такое же рассуждение
справедливо и для двух других медиан, то центр тяжести треугольника лежит
в точке пересечения его медиан. При задании вершин треугольника их координатами
получим
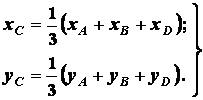 (1.22)
(1.22)
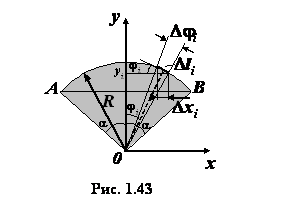
Центр тяжести дуги окружности. Разобьем дугу 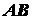 на бесконечно малые элементарные дуги (рис. 1.43).
на бесконечно малые элементарные дуги (рис. 1.43).
Очевидно, что 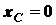 .
.
Воспользуемся формулой
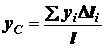 .
.
С помощью рис. 1.43 имеем
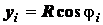 ;
;
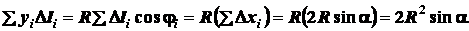 ,
,
где 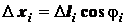 ;
;
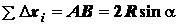 ;
; 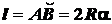 .
.
Окончательно получаем
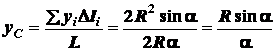 . (1.23)
. (1.23)
Центр тяжести площади сектора. 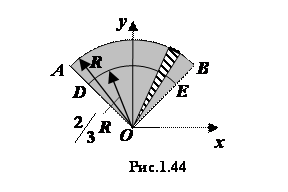 Мысленно разобьем сектор
Мысленно разобьем сектор 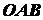 радиусами, проведенными из центра
радиусами, проведенными из центра 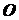 , на бесконечно малые
секторы, один из которых показан на чертеже (см. рис. 1.44). Каждый такой сектор
можно рассматривать как треугольник, и поэтому его центр тяжести расположен на стоянии
, на бесконечно малые
секторы, один из которых показан на чертеже (см. рис. 1.44). Каждый такой сектор
можно рассматривать как треугольник, и поэтому его центр тяжести расположен на стоянии 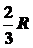 от центра
от центра 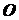 . Геометрическим местом
центров тяжести всех этих секторов является дуга
. Геометрическим местом
центров тяжести всех этих секторов является дуга 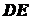 , центр тяжести которой
и совпадает с центром тяжести данного сектора
, центр тяжести которой
и совпадает с центром тяжести данного сектора 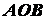 . По формуле (1.23),
заменяя
. По формуле (1.23),
заменяя 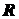 на
на 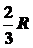 , получаем
, получаем
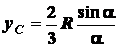 .
(1.24)
.
(1.24)
В частности, для полуокружности и полукруга 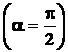 по формулам
по формулам
по формулам (1.22) и (1.23) будем иметь соответственно
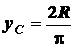
и
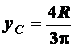 ,
,
что совпадает с результатами, полученными при решении задачи 1.13.
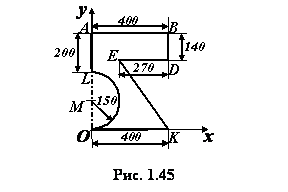
Задача 1.14. Определить координаты центра
тяжести тонкой однородной пластинки, форма и размеры которой указаны на рис. 1.45.
Решение. Будем рассматривать данную пластинку
как совокупность полного прямоугольника без вырезов, прямоугольного треугольника
и полукруга с отрицательными площадями, которые наложены в местах вырезов. Для
удобства дальнейших вычислений найдем неизвестные длины отрезков 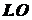 ,
, 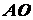 и
и 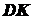 :
:
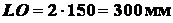 ;
;
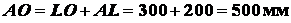 ;
;
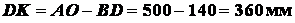 .
.
Найдем
площади и координаты центров тяжести этих частей.
 Для прямоугольника
Для прямоугольника
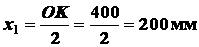 ;
;
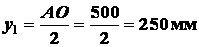 ;
;
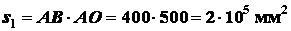 .
.
Для треугольника
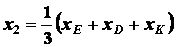 ;
; 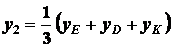 .
.
Так как
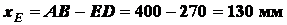 ;
; 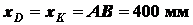 ;
; 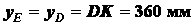 ;
; 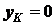 ,
,
координаты центра
тяжести треугольника имеют вид
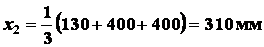 ;
; 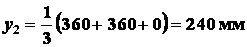 ,
,
площадь треугольника
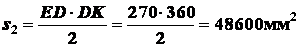 .
.
Для полукруга
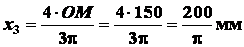 ;
;
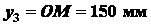 ;
;
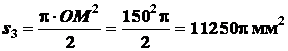 .
.
Следовательно, по формулам (1.18):
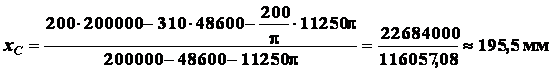 ;
;
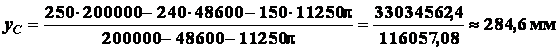 .
.
Центр тяжести прямого кругового
конуса. Пусть дан прямой круговой конус (рис. 1.46)
с высотой 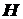 и радиусом основания
и радиусом основания 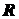 . Ось конуса
. Ось конуса 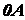 примем за координатную ось
примем за координатную ось 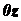 . Разобьем мысленно конус
на
. Разобьем мысленно конус
на 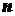 тонких слоев
тонких слоев 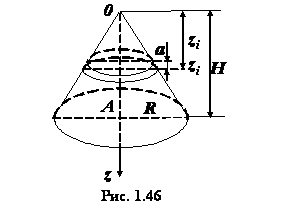 сечениями, параллельными основанию. Принимая приближенно каждый слой за
цилиндрический диск с радиусом основания
сечениями, параллельными основанию. Принимая приближенно каждый слой за
цилиндрический диск с радиусом основания 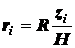 ,
, 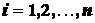 , и толщиной
, и толщиной 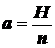 , получим, что его объем
, получим, что его объем
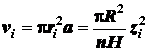 .
.
Отсчитывая номера слоев от вершины
конуса, имеем
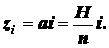
Тогда
по формуле (1.17) получим приближенно
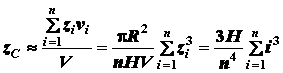 ,
,
где 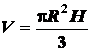 - объем конуса.
- объем конуса.
Известно,
что
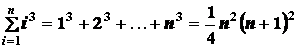 .
.
Поэтому
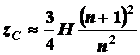 .
.
Переходя
к пределу при 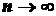 и учитывая, что
и учитывая, что
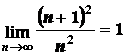 ,
,
получим точное значение координаты
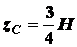 .
.
Аналогично
можно показать, что и у любой пирамиды центр тяжести лежит на отрезке, соединяющем
ее вершину с центром тяжести основания, на расстоянии от вершины, равном 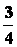 длины этого отрезка.
длины этого отрезка.
Более
эффективно подобные задачи решаются при помощи аппарата интегрального исчисления.