Г л а в а
I
КИНЕМАТИКА ТОЧКИ
§ 1. Введение
в кинематику
Кинематикой называют раздел теоретической механики, в котором
изучается движение материальных тел с геометрической точки зрения независимо
от приложенных сил.
Положение движущегося
тела в пространстве всегда определяется по отношению к любому другому неизменяемому
телу, называемому телом отсчета. Система координат, неизменно связанная
с телом отсчета, называется системой отсчета. В механике Ньютона время
считается абсолютным и не связанным с движущейся материей. В соответствии
с этим оно протекает одинаково во всех системах отсчета независимо от их движения.
Основной единицей измерения времени является секунда (с).
Если положение тела
по отношению к выбранной системе отсчета с течением времени не изменяется, то
говорят, что тело относительно данной системы отсчета находится в покое.
Если же тело изменяет свое положение относительно выбранной системы отсчета,
то говорят, что оно движется по отношению к этой системе. Тело может находиться
в состоянии покоя по отношению к одной системе отсчета, но двигаться (и притом
совершенно различным образом) по отношению к другим системам
отсчета. Например, пассажир, неподвижно сидящий на скамье движущегося поезда,
покоится относительно системы отсчета, связанной с вагоном, но движется по отношению
к системе отсчета, связанной с Землей. Точка, лежащая на поверхности катания
колеса, движется по отношению к системе отсчета, связанной с вагоном, по окружности,
а по отношению к системе отсчета, связанной с Землей, по циклоиде; та же точка
покоится по отношению к системе координат, связанной с колесной парой.
Таким образом, движение
или покой тела могут рассматриваться лишь по отношению к какой-либо выбранной
системе отсчета. Задать движение тела относительно какой-либо системы
отсчета - значит дать функциональные
зависимости, с помощью которых можно определить положение тела в любой момент
времени относительно этой системы. Различные точки одного и того же тела по
отношению к выбранной системе отсчета движутся по-разному. Например, по отношению
к системе, связанной с Землей, точка поверхности катания колеса движется по циклоиде,
а центр колеса - по прямой. Поэтому изучение кинематики
начинают с кинематики точки.
§ 2. Способы задания движения точки
Движение точки
может быть задано тремя способами: естественным, векторным и координатным.
При естественном
способе задания движения дается траектория, т. е. линия, по которой движется точка
(рис.2.1).  На этой траектории выбирается
некоторая точка
На этой траектории выбирается
некоторая точка  , принимаемая за начало
отсчета. Выбираются положительное и отрицательное направления отсчета дуговой
координаты
, принимаемая за начало
отсчета. Выбираются положительное и отрицательное направления отсчета дуговой
координаты  , определяющей положение
точки на траектории. При движении точки расстояние
, определяющей положение
точки на траектории. При движении точки расстояние  будет изменяться. Поэтому, чтобы определить положение точки в любой момент
времени, достаточно задать дуговую координату
будет изменяться. Поэтому, чтобы определить положение точки в любой момент
времени, достаточно задать дуговую координату  как функцию времени:
как функцию времени:
 . (2.1)
. (2.1)
Это равенство называется уравнением
движения точки по данной траектории.
Итак, движение точки
в рассматриваемом случае определяется совокупностью следующих данных: траектории
точки, положения начала отсчета дуговой координаты, положительного и отрицательного
направлений отсчета и функции  .
.
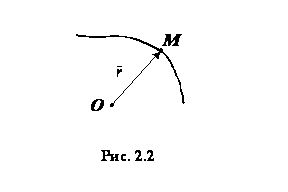 При векторном способе задания
движения точки положение точки
При векторном способе задания
движения точки положение точки 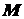 определяется величиной и направлением радиуса-вектора
определяется величиной и направлением радиуса-вектора
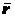 , проведенного из неподвижного
центра
, проведенного из неподвижного
центра  в данную точку (рис. 2.2). При движении точки ее радиус-вектор
в данную точку (рис. 2.2). При движении точки ее радиус-вектор 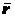 изменяется по величине и направлению. Поэтому, чтобы определить положение
точки в любой момент времени, достаточно задать ее радиус-вектор
изменяется по величине и направлению. Поэтому, чтобы определить положение
точки в любой момент времени, достаточно задать ее радиус-вектор 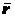 как функцию времени:
как функцию времени:
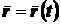 . (2.2)
. (2.2)
Это равенство называется векторным
уравнением движения точки.
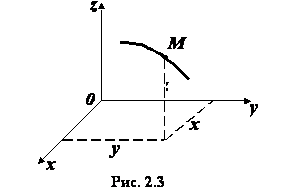 При координатном способе задания движения положение
точки по отношению к выбранной системе отсчета определяется при помощи прямоугольной
системы декартовых координат (рис. 2.3). При движении точки ее координаты изменяются
с течением времени. Поэтому, чтобы определить положение точки в любой момент времени,
достаточно задать координаты
При координатном способе задания движения положение
точки по отношению к выбранной системе отсчета определяется при помощи прямоугольной
системы декартовых координат (рис. 2.3). При движении точки ее координаты изменяются
с течением времени. Поэтому, чтобы определить положение точки в любой момент времени,
достаточно задать координаты 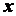 ,
, 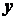 ,
, 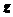 как функции времени:
как функции времени:
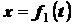 ;
;
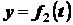 ;
;
 . (2.3)
. (2.3)
Эти равенства называются уравнениями
движения точки в прямоугольных декартовых координатах. Движение точки
в плоскости определяется двумя уравнениями системы (2.3), прямолинейное движение
— одним.
Между
тремя описанными способами задания движения существует взаимная связь, что позволяет
от одного способа задания движения перейти к другому. В этом легко убедиться,
например, при рассмотрении перехода от координатного способа задания движения к векторному.
Положим, что движение
точки задано в виде уравнений (2.3). Имея в виду, что
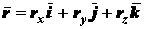
и
 ;
; 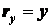 ;
;
 ,
,
можно записать
 .
.
А это и есть уравнение вида
(2.2).
Задача 2.1. Найти уравнение движения и
траекторию средней точки 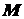 шатуна, а также уравнение движения ползуна
шатуна, а также уравнение движения ползуна 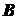 кривошипно-ползунного механизма (рис. 2.4), если
кривошипно-ползунного механизма (рис. 2.4), если
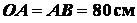 ;
;  .
.
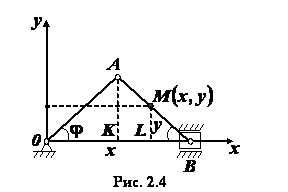 Решение. Положение точки
Решение. Положение точки 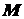 определяется двумя координатами
определяется двумя координатами 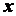 и
и 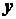 . Из
рис. 2.4 видно, что
. Из
рис. 2.4 видно, что
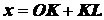 ,
, 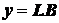 .
.
Тогда из  и
и 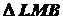 :
:
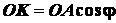 ;
; 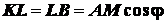 ;
; 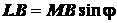 .
.
Подставляя значения 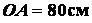 ,
, 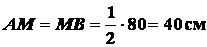 и
и  ,
получаем уравнения движения точки
,
получаем уравнения движения точки 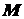 :
:
 ;
;
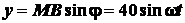
или
 ;
;
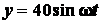 .
.
Чтобы найти уравнение траектории точки в явной форме, надо
исключить из уравнений движения время 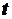 . С этой целью проведем
необходимые преобразования в полученных выше уравнениях движения:
. С этой целью проведем
необходимые преобразования в полученных выше уравнениях движения:
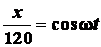 ;
; 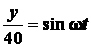 .
.
Возводя в квадрат
и складывая левые и правые части этих уравнений, получим
уравнение траектории в виде
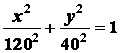 .
.
Следовательно, траектория точки
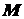 - эллипс.
- эллипс.
Ползун 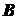 движется прямолинейно. Координату
движется прямолинейно. Координату 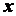 , определяющую положение
точки, можно записать в виде
, определяющую положение
точки, можно записать в виде
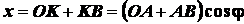
или
 .
.
§ 3. Понятие скорости точки
Скорость точки является характеристикой быстроты и направления
ее движения.
Пусть точка 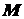 (рис. 2.5, а) движется по криволинейной траектории согласно закону
(рис. 2.5, а) движется по криволинейной траектории согласно закону  . Положим, что в момент
времени
. Положим, что в момент
времени 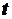 точка занимает положение
точка занимает положение 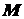 , а в момент времени
, а в момент времени
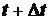 положение
положение 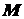 ,
пройдя за время
,
пройдя за время  путь
путь  .
.
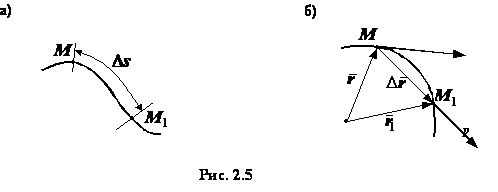
Отношение приращения
дуговой координаты  к промежутку времени
к промежутку времени  , за которое произошло
это приращение, называется средней скоростью точки за время
, за которое произошло
это приращение, называется средней скоростью точки за время 
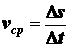 . (2.4)
. (2.4)
Очевидно, что, чем меньше промежуток
времени  , тем ближе значение
, тем ближе значение
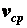
подходит к величине действительной
скорости точки в момент времени 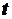 .
.
Скоростью называется предел 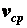 при
при 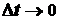 :
:
 ;
;
 . (2.5)
. (2.5)
Итак, величина скорости точки
равна производной от расстояния (дуговой координаты) по времени. Следовательно,
она измеряется в единицах длины, отнесенных к единице времени (м/с, см/с). Формула (2.5) определяет величину скорости
точки.
Чтобы знать не только
величину скорости, но и ее направление, введем понятие вектора скорости. Для этого
будем определять движение в векторной форме (2.2). В момент времени 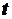 положение точки
положение точки 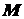 (рис. 2.5, б) определяется радиусом-вектором
(рис. 2.5, б) определяется радиусом-вектором
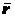 , а в момент времени
, а в момент времени
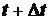 , соответствующий положению
, соответствующий положению
 , -
радиусом-вектором
, -
радиусом-вектором  .
.
Отношение приращения
радиуса-вектора 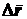 к промежутку времени
к промежутку времени  , в течение которого
произошло это приращение, называется вектором средней скорости точки за
время
, в течение которого
произошло это приращение, называется вектором средней скорости точки за
время  , т. е.
, т. е.
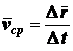 . (2.6)
. (2.6)
Направление вектора
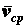 совпадает с направлением вектора
совпадает с направлением вектора 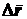 . Рассматривая предел
отношения (2.6) при приближении
. Рассматривая предел
отношения (2.6) при приближении  к нулю, получим
к нулю, получим
 .
.
Из равенства (2.7)
следует, что вектор 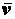 всегда направлен по касательной
всегда направлен по касательной
к траектории в точке 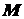 .
.
Итак, вектор
скорости точки равен производной от радиуса-вектора по
времени.
Равенство (2.7) можно представить в виде
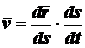 .
.
Вектор 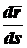 , направлен по касательной
к траектории в сторону возрастания дуговой координаты
, направлен по касательной
к траектории в сторону возрастания дуговой координаты  и равен по модулю единице. Он называется единичным вектором касательной
и обозначается
и равен по модулю единице. Он называется единичным вектором касательной
и обозначается 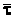 . Следовательно, можно
записать
. Следовательно, можно
записать
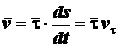 .
.
Отсюда следует, что определенная равенством (2.5)
алгебраическая величина  представляет собой проекцию вектора скорости
представляет собой проекцию вектора скорости 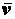 на направление единичного вектора касательной.
на направление единичного вектора касательной.
Задача 2.2. Точка 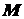 обода маховика в период пуска движется согласно уравнению
обода маховика в период пуска движется согласно уравнению 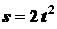 , где
, где 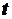 - в
- в  ,
,  - в
- в  . Определить скорость
точки, среднюю скорость за
. Определить скорость
точки, среднюю скорость за 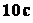 и скорость через
и скорость через 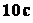 после начала движения.
после начала движения.
Решение. Скорость точки равна первой производной пути по времени
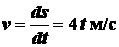 .
.
Отсюда
имеем, что через десять секунд после начала движения, т.е. при
 , скорость точки составляет
, скорость точки составляет
 .
.
Средняя скорость за некоторый
промежуток времени равна отношению перемещения к промежутку времени, за которое
это перемещение произошло. В нашем случае, за десять секунд точка прошла расстояние
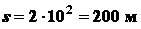 , следовательно,
, следовательно,
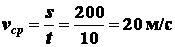 .
.
§ 4. Определение скорости при координатном способе
задания движения
Пусть движение точки задано
уравнениями движения в прямоугольных
декартовых координатах:
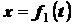 ;
;
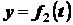 ;
;
 .
.
Так как
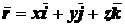 ,
,
то на основании равенства (2.7) получим
 .
.
 При дифференцировании принимается
во внимание, что единичные векторы
При дифференцировании принимается
во внимание, что единичные векторы 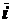 ,
, 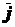 ,
,  и постоянны по величине и направлению. Последнее вытекает из того, что
система координат неизменно связана с телом отсчета. Коэффициента при
и постоянны по величине и направлению. Последнее вытекает из того, что
система координат неизменно связана с телом отсчета. Коэффициента при 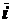 ,
, 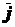 ,
,  в полученном равенстве представляют собой проекции
вектора скорости на оси
в полученном равенстве представляют собой проекции
вектора скорости на оси 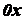 ,
,  ,
,  . Следовательно,
. Следовательно,
 ;
;
 ;
;
 .
.
Таким образом, проекции вектора
скорости точки на координатные оси равны первым производным от соответствующих
координат точки по времени. Модуль скорости (рис. 2.6) вычисляется по формуле
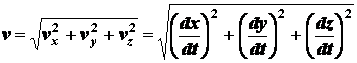 .
(2.9)
.
(2.9)
Направление вектора скорости
определяется следующим образом:
 ;
;
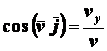 ;
;
 .
(2.10)
.
(2.10)
Задача 2.3. Движение точки задано уравнениями:
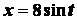 ;
;
 ,
,
где
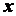 и
и 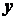 - в
- в  ,
, 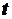 , - в
, - в  . Определить величину
и направление скорости в
. Определить величину
и направление скорости в
начале и через 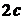 после начала движения.
после начала движения.
Решение. Находим проекции
вектора скорости на координатные оси:
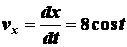 ;
;
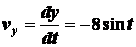 .
.
Определяем модуль вектора скорости
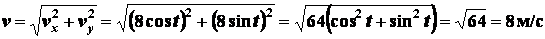
и его направление
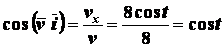 ;
;
 .
.
В начальный момент времени, т.е. при
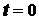 , получаем
, получаем  . Соответственно
. Соответственно
 ;
; 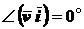 ;
; 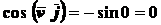 ;
;  ,
,
т.е.
направление вектора скорости совпадает с направлением оси 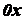 .
.