§ 5. Понятие
ускорения точки
Ускорение точки характеризует быстроту изменения ее скорости. Положим,
что точка движется по криволинейной траектории (рис. 2.7). В момент времени 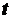 она занимает положение
она занимает положение  и имеет скорость
и имеет скорость 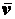 . В момент времени
. В момент времени 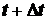 точка занимает положение
точка занимает положение  и имеет скорость
и имеет скорость 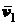 . Перенося вектор
. Перенося вектор 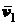
 в точку
в точку  и соединяя концы векторов и
и соединяя концы векторов и 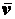 и
и 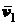 , получим вектор
, получим вектор  , выражающий приращение
вектора скорости за время
, выражающий приращение
вектора скорости за время  .
.
Отношение приращения вектора скорости  промежутку времени
промежутку времени  , в течение которого
произошло это приращение, называется средним ускорением
, в течение которого
произошло это приращение, называется средним ускорением
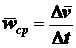 . (2.11)
. (2.11)
Рассмотрим предел выражения (2.11) при приближении  к нулю. Получим истинное ускорение точки в момент времени
к нулю. Получим истинное ускорение точки в момент времени 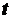 , т. е. в положении
, т. е. в положении  ,
,
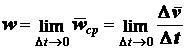 ;
;
 .
(2.12)
.
(2.12)
Таким образом, вектор ускорения равен первой производной
от вектора скорости по времени или второй производной от радиуса-вектора
по времени.
Заметим, что вектор  находится в плоскости
находится в плоскости  (рис. 2.7), проходящей через касательную к траектории в точке
(рис. 2.7), проходящей через касательную к траектории в точке  и параллельной касательной в точке
и параллельной касательной в точке  . При
. При  ,
стремящемся к нулю, плоскость
,
стремящемся к нулю, плоскость  вращается вокруг касательной
вращается вокруг касательной  , будучи все время параллельной
вектору
, будучи все время параллельной
вектору 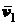 . Плоскость, с которой
совпадает предельное положение плоскости
. Плоскость, с которой
совпадает предельное положение плоскости  при
при  называется соприкасающейся плоскостью к кривой в точке
называется соприкасающейся плоскостью к кривой в точке  . Вектор
. Вектор  находится все время в плоскости
находится все время в плоскости  и направлен в сторону вогнутости траектории. Поэтому вектор
и направлен в сторону вогнутости траектории. Поэтому вектор  лежит в соприкасающейся плоскости и тоже направлен в сторону вогнутости
траектории. Ускорение измеряется в
лежит в соприкасающейся плоскости и тоже направлен в сторону вогнутости
траектории. Ускорение измеряется в 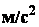 ,
,  .
.
§ 6. Определение
ускорения при координатном
способе задания движения
При определении ускорения в случае задания движения в прямоугольных
координатах, т. е. в виде
 ;
;
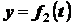 ;
;
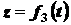 ,
,
последовательность операций аналогична действиям, описанным в § 5. Сначала найдем проекции вектора ускорения на координатные
оси:
 ;
;
 ;
;
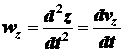 .
(2.13)
.
(2.13)
Проекции ускорения точки на координатные оси равны вторым
производным от соответствующих координат по времени или первым производным
по времени от проекций скорости на соответствующие оси.
Модуль ускорения определяется по формуле
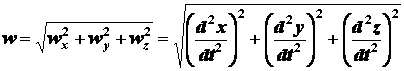 .
(2.14)
.
(2.14)
Направление вектора ускорения определяется направляющими
косинусами:
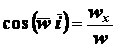 ;
;
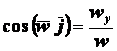 ;
;
 .
(2.15)
.
(2.15)
Задача 2.5. Движение точки задано уравнениями:
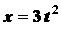 ;
;  ,
,
где 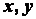 - в
- в 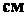 ,
, 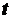 - в
- в  . Определить
величину и направление ускорения при
. Определить
величину и направление ускорения при 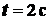 .
.
Решение. Находим проекции ускорения на координатные
оси:
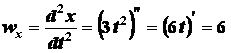 ;
;
 .
.
Как видно, проекции ускорения не зависят от времени движения, значит
ускорение тоже постоянно
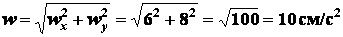
и его направление
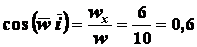 ;
;
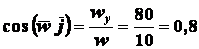 .
.
§ 7. Разложение
вектора ускорения по естественным
осям траектории
Проведем в точке  кривой
кривой 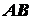 соприкасающуюся плоскость (рис.2.8), определение которой дано в разделе
§ 6, и плоскость, перпендикулярную к касательной.
Эта плоскость называется нормальной плоскостью. Линия пересечения нормальной
и соприкасающейся
соприкасающуюся плоскость (рис.2.8), определение которой дано в разделе
§ 6, и плоскость, перпендикулярную к касательной.
Эта плоскость называется нормальной плоскостью. Линия пересечения нормальной
и соприкасающейся плоскостей называется главной нормалью кривой. Прямая, перпендикулярная к главной нормали и касательной,
называется бинормалью.
плоскостей называется главной нормалью кривой. Прямая, перпендикулярная к главной нормали и касательной,
называется бинормалью.
Рассмотрим три взаимно перпендикулярные оси: касательную,
направленную в сторону возрастания дуговой координаты; главную нормаль, направленную
в сторону вогнутости кривой; бинормаль, направленную по отношению к двум другим
осям подобно тому, как ось 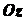 направлена по отношению к осям
направлена по отношению к осям  и
и  . Эти три оси называются
естественными осями кривой. Единичные векторы этих осей принято обозначать соответственно
. Эти три оси называются
естественными осями кривой. Единичные векторы этих осей принято обозначать соответственно
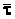 ,
, 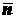 и
и 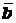 .
.
Из курса высшей математики известно, что угол поворота
касательной при переходе точки из одного положения в другое называется углом смежности.
Предел отношения угла смежности к приращению дуговой координаты  , когда она стремится
к нулю, называется кривизной
, когда она стремится
к нулю, называется кривизной  кривой в точке
кривой в точке 
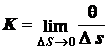 . (2.16)
. (2.16)
Величина 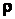 , обратная кривизне кривой,
называется радиусом кривизны:
, обратная кривизне кривой,
называется радиусом кривизны:
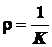 . (2.17)
. (2.17)
Представим вектор скорости 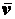 в виде произведения его проекции на
в виде произведения его проекции на
касательную и единичного вектора 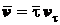 . Тогда
. Тогда
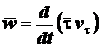 .
.
Величина единичного вектора 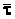 постоянна, направление же его при движении точки вдоль ее траектории меняется.
Поэтому вектор
постоянна, направление же его при движении точки вдоль ее траектории меняется.
Поэтому вектор 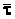 нельзя рассматривать как постоянный и его производная по времени не равна
нулю. Дифференцируя последнее выражение как произведение двух функций времени,
получим
нельзя рассматривать как постоянный и его производная по времени не равна
нулю. Дифференцируя последнее выражение как произведение двух функций времени,
получим
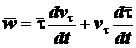 . (2.18)
. (2.18)
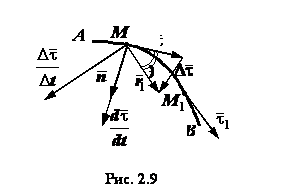 Выясним, чему равна производная
Выясним, чему равна производная 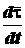 . Возьмем на кривой
. Возьмем на кривой 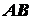 (рис. 2.9) два положения движущейся точки
(рис. 2.9) два положения движущейся точки  и
и  , соответствующие моментам
времени
, соответствующие моментам
времени 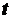 и
и 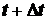 .
Орты касательной в этих точках соответственно
.
Орты касательной в этих точках соответственно 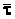 и
и  . Перенося
. Перенося  в точку
в точку  , определим приращение
орта
, определим приращение
орта 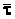
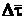 . Как видно из рисунка,
. Как видно из рисунка,
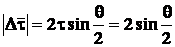 ;
;
 .
.
Следовательно,
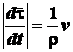 .
.
Из рис. 2.9 видно, что угол, образованный вектором 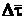 и касательной,
и касательной, 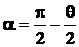 .
При
.
При 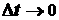
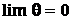 и поэтому
и поэтому 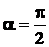 . Это значит, что вектор
. Это значит, что вектор
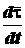 направлен по нормали к траектории, а так как он лежит в соприкасающейся
плоскости, то эта нормаль является главной нормалью.
направлен по нормали к траектории, а так как он лежит в соприкасающейся
плоскости, то эта нормаль является главной нормалью.
Значит,
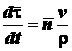 ,
,
и равенство (2.18) примет вид
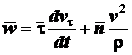 . (2.19)
. (2.19)
Первое слагаемое суммы (2.19) называется касательным ускорением
точки 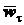 , второе - нормальным
ускорением
, второе - нормальным
ускорением  . Тогда
. Тогда
 . (2.20)
. (2.20)
Проекции ускорения на касательную и главную нормаль соответственно
равны:
 ; (2.21)
; (2.21)
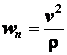 . (2.22)
. (2.22)
Проекция ускорения на бинормаль всегда равна нулю.
Модуль полного ускорения точки определяется через ее касательное и
нормальное ускорения
 . (2.23)
. (2.23)
Задача 2.5. Уравнения движения пальца кривошипа
дизеля в период пуска имеют вид:
 ;
; 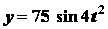 ,
,
где 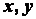 - в
- в 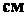 ,
, 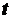 - в
- в  . Найти скорость, касательное
и нормальное ускорения пальца.
. Найти скорость, касательное
и нормальное ускорения пальца.
Решение. Находим проекции скорости точки на
координатные оси. Так как
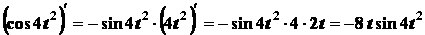 ;
;
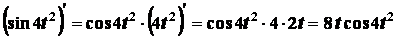 ,
,
получаем
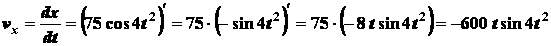 ;
;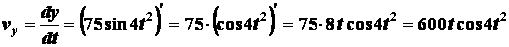 .
.
Определяем модуль вектора скорости
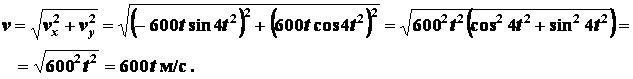
Находим проекции ускорения на координатные оси:
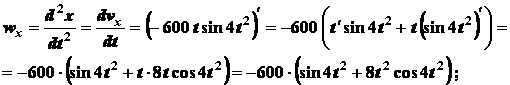
 .
.
Определяем модуль вектора ускорения. Так как
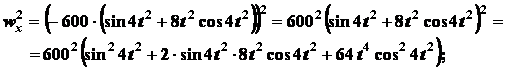
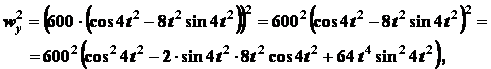
то
 .
.
Определяем модуль касательного ускорения:
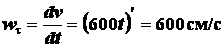 ,
,
тогда модуль нормального ускорения:

§ 8. Некоторые
частные случаи движения точки
Пользуясь полученными результатами, исследуем зависимость
значений ее нормального и касательного ускорений от характера движения точки.
При равномерном движении,
когда численное значение скорости 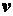 постоянно, касательное ускорение
постоянно, касательное ускорение 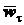 обращается в нуль. Оно отлично от нуля только при неравномерном движении
и поэтому характеризует изменение скорости по величине.
обращается в нуль. Оно отлично от нуля только при неравномерном движении
и поэтому характеризует изменение скорости по величине.
При прямолинейном движении, когда радиус кривизны траектории 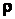 равен бесконечности, нормальное ускорение обращается в нуль. Оно отлично
от нуля только при криволинейном движении и, следовательно, характеризует
изменение скорости по направлению.
равен бесконечности, нормальное ускорение обращается в нуль. Оно отлично
от нуля только при криволинейном движении и, следовательно, характеризует
изменение скорости по направлению.
Обе составляющие ускорения обращаются в нуль только при равномерном
и прямолинейном движении.
Неравномерное движение точки называется ускоренным,
если модуль скорости возрастает, и замедленным - в противоположном случае. Легко
доказать, что движение является ускоренным, если знаки величин 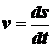 и
и  одинаковы, и замедленным, если эти знаки различны. При ускоренном движении
вектор касательного ускорения направлен в ту же сторону, что и скорость, при замедленном
- в противоположную сторону.
одинаковы, и замедленным, если эти знаки различны. При ускоренном движении
вектор касательного ускорения направлен в ту же сторону, что и скорость, при замедленном
- в противоположную сторону.
Движение называется равнопеременным в том случае,
если касательное
ускорение постоянно, т. е.
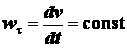 , (2.24)
, (2.24)
откуда
 .
.
Интегрируя последнее выражение и имея в виду, что при 
 , получим
, получим
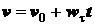 . (2.25)
. (2.25)
Формула (2.25) определяет скорость равнопеременного движения. Подставляем
в нее значение 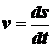 . Интегрируя и имея в
виду, что при
. Интегрируя и имея в
виду, что при 
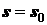 , получим
, получим
 . (2.26)
. (2.26)
Выражение (2.26) называют уравнением равнопеременного движения точки по
траектории.